【题目】观察等式：
；
；
……，按一定规律排列的一组数：
、
、
、……、
、
。若=a，用含a的式子表示这组数的和是__________.
【答案】2a2-a．
【解析】
由等式：2+22=23-2；2+22+23=24-2；2+22+23+24=25-2，得出规律：2+22+23+…+2n=2n+1-2，那么250+251+252+…+299+2100=（2+22+23+…+2100）-（2+22+23+…+249），将规律代入计算即可．
∵2+22=23-2；
2+22+23=24-2；
2+22+23+24=25-2；
…
∴2+22+23+…+2n=2n+1-2，
∴250+251+252+…+299+2100
=（2+22+23+…+2100）-（2+22+23+…+249）
=（2101-2）-（250-2）
=2101-250，
∵250=a，
∴2101=（250）22=2a2，
∴原式=2a2-a．
故答案为：2a2-a．
科目：初中数学 来源： 题型：
【题目】甲、乙两人分别从A、B两地同时出发，相向而行，匀速前往B地、A地，两人相遇时停留了4min，又各自按原速前往目的地，甲、乙两人之间的距离y（m）与甲所用时间x（min）之间的函数关系如图所示．有下列说法：
①A、B之间的距离为1200m； ②乙行走的速度是甲的1.5倍；③ b=960； ④ a=34．
以上结论正确的有（ ）
A. ①② B. ①②③ C. ①③④ D. ①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
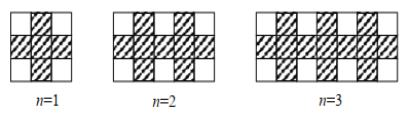
（1）铺第5个图形用黑色正方形瓷砖 块；
（2）按照此方式铺下去，铺第 n 个图形用黑色正方形瓷砖 块；（用含 n的代数式表示）
（3）若黑、白两种颜色的瓷砖规格都为（ 长0.5米宽0.5米），且黑色正方形瓷砖每块价格 25 元，白色正方形瓷砖每块价格30元，若按照此方式恰好铺满该小路某一段（该段小路的总面积为 18.75 平方米），求该段小路所需瓷砖的总费用．
查看答案和解析>>
科目：初中数学 来源： 题型：
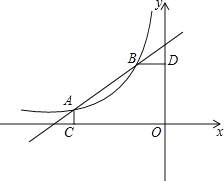
【题目】如图，在平面直角坐标系中，直线y=
x+
与反比例函数y=
(x<0)的图象交于A(-4,a)、B(-1，b)两点，AC⊥x轴于C，BD⊥y轴于D．
（1）求a 、b及k的值；
（2）连接OA，OB，求△AOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如
就是完全对称式(代数式中
换成b，b换成，代数式保持不变).下列三个代数式：①
；②
；③
．其中是完全对称式的是（ ）
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图在平行四边形ABCD中，BC=2AB，CE⊥AB于E，F为AD的中点，若∠AEF=54，则∠B=（ ）
A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把四张大小相同的长方形卡片（如图①）按图②、图③两种放法放在一个底面为长方形（长比宽多
）的盒底上，底面为被卡片覆盖的部分用阴影表示，若记图②中阴影部分的周长为
，图③中阴影部分的周长为
，则
________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市有
两种出租车.
的计价方式为：当行驶路程不超过
千米时收费
元，每超过
千米则另外收费
元（不足千米按千米收费）；
的计价方式为：当行驶路程不超过千米时收费
元，每超过千米则另外收费
元（不足千米按千米收费）．某人到该市出差，需要乘坐的路程为
千米．
（1）当
时，请分别求出乘坐两种出租车的费用；
（2）①此人若乘坐种出租车比乘坐种出租车的费用省元，则求的值；
②某人乘坐的路程大于千米，请帮他规划如何选择乘坐哪种出租车较合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
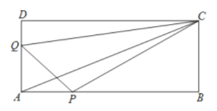
【题目】在长方形ABCD中，AB=3a厘米，BC=a厘米，点P沿AB边从点A开始向终点B以2厘米/秒的速度移动，点Q沿DA边从点D开始向终点A以1厘米/秒的速度移动，如果P、Q同时出发，以t（秒）表示移动的时间，
（1）用含有a、t的代数式表示△APC的面积
（2）求△PQC的面积（用含有a、t的代数式表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com