
【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
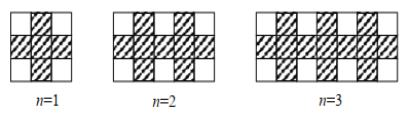
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
【答案】(1)21;(2)4n+1;(3)2005元.
【解析】
(1)根据题意构造出第五个图形的形状,数黑色正方形瓷砖的块数,即可得出答案;
(2)多画几个图形,总结规律,即可得出答案;
(3)分别求出黑白两种瓷砖的块数,乘以各自的价格即可得出答案.
解:(1)由题意可得,铺第5个图形用黑色正方形瓷砖21块;
(2)铺第1个图形用黑色正方形瓷砖5块
铺第2个图形用黑色正方形瓷砖9=5+4块
铺第3个图形用黑色正方形瓷砖13=5+4+4块
铺第4个图形用黑色正方形瓷砖17=5+4+4+4块
铺第5个图形用黑色正方形瓷砖21=5+4+4+4+4块
……
∴铺第n个图形用黑色正方形瓷砖5+4(n-1)=4n+1块
故答案为:4n+1.
(3)18.75÷(0.5×0.5)=75(块)
由题意可得,铺第n个图形共用正方形瓷砖9+6(n-1)=6n+3块,铺第n个图形用白色正方形瓷砖4+2(n-1)=2n+2块
6n+3=75,解得:n=12
可知,第12个图形用黑色正方形:4×12+1=49块,用白色正方形:2×12+2=26块
所以总费用=49×25+26×30=2005(元)
答:该段小路所需瓷砖的总费用为2005元.


科目:初中数学 来源: 题型:
【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) | 频数(人数) | 频率 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | c | 1 |
(1)统计表中的a= ,b= ,c= ;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
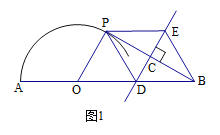
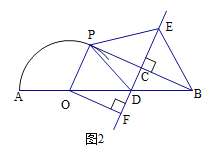
【题目】如图,点O在线段AB上,(不与端点A、B重合),以点O为圆心,OA的长为半径画弧,线段BP与这条弧相切与点P,直线CD垂直平分PB,交PB于点C,交AB于点D,在射线DC上截取DE,使DE=DB。已知AB=6,设OA=r。
(1)求证:OP∥ED;
(2)当∠ABP=30°时,求扇形AOP的面积,并证明四边形PDBE是菱形;
(3)过点O作OF⊥DE于点F,如图所示,线段EF的长度是否随r的变化而变化?若不变,直接写出EF的值;若变化,直接写出EF与r的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
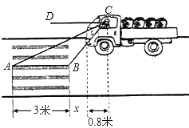
【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
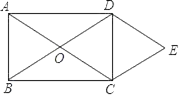
【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若点E到CD的距离为2,CD=3,试求出矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示).
问题探究
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
(3)①如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
②如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:
我们知道,|m|= .现在我们可以用这一结论来化简含有绝对值的代
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令 m+1=0 和 m﹣2=0,分别求得 m=﹣1,m=2(称﹣1,2 分别为|m+1|与|m﹣2|的零点值).在实数范围内, 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况:
(1)当 m<﹣1 时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2 时,原式=m+1﹣(m﹣2)=3;
(3)当 m≥2 时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com