
【题目】问题提出
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示).
问题探究
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
(3)①如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
②如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.

【答案】(1)CB的延长线上,a+b;(2)①CD=BE,②9;(3)P(2﹣![]() ,
,![]() )(4)AC的最大值为2
)(4)AC的最大值为2![]() +2
+2![]()
【解析】试题分析:(1)根据点A位于CB的延长线上时,线段AC的长取得最大值,即可得到结论;
(2)①根据等边三角形的性质得到AD=AB,AC=AE,∠BAD=∠CAE=60°,推出△CAD≌△EAB,根据全等三角形的性质得到CD=BE;②由于线段BE长的最大值=线段CD的最大值,根据(1)中的结论即可得到结果;
(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,得到△APN是等腰直角三角形,根据全等三角形的性质得到PN=PA=2,BN=AM,根据当N在线段BA的延长线时,线段BN取得最大值,即可得到最大值为2![]() +3;过P作PE⊥x轴于E,根据等腰直角三角形的性质,即可得到结论;
+3;过P作PE⊥x轴于E,根据等腰直角三角形的性质,即可得到结论;
(4)如图4中,以BC为边作等边三角形△BCM,由△ABC≌△DBM,推出AC=MD,推出欲求AC的最大值,只要求出DM的最大值即可,由BC=4![]() =定值,∠BDC=90°,推出点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大;
=定值,∠BDC=90°,推出点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大;
试题解析:解:(1)∵点A为线段BC外一动点,且BC=a,AB=b,∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b.故答案为:CB的延长线上,a+b;
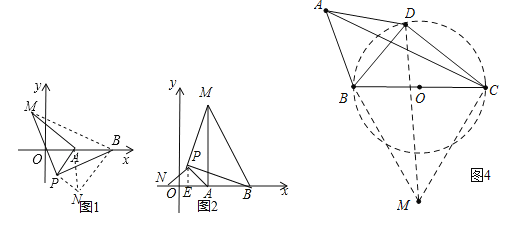
(2)①CD=BE,理由:∵△ABD与△ACE是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.在△CAD与△EAB中,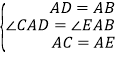 ,∴△CAD≌△EAB(SAS),∴CD=BE;
,∴△CAD≌△EAB(SAS),∴CD=BE;
②∵线段BE长的最大值=线段CD的最大值,∴由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,∴最大值为BD+BC=AB+BC=3+6=9;
(3)如图1,连接BM.∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN是等腰直角三角形,∴PN=PA=2,BN=AM.∵A的坐标为(2,0),点B的坐标为(5,0),∴OA=2,OB=5,∴AB=3,∴线段AM长的最大值=线段BN长的最大值,∴当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN.∵AN=![]() AP=2
AP=2![]() ,∴最大值为2
,∴最大值为2![]() +3;
+3;
如图2,过P作PE⊥x轴于E.∵△APN是等腰直角三角形,∴PE=AE=![]() ,∴OE=BO﹣AB﹣AE=5﹣3﹣
,∴OE=BO﹣AB﹣AE=5﹣3﹣![]() =2﹣
=2﹣![]() ,∴P(2﹣
,∴P(2﹣![]() ).
).
(4)如图4中,以BC为边作等边三角形△BCM.∵∠ABD=∠CBM=60°,∴∠ABC=∠DBM.∵AB=DB,BC=BM,∴△ABC≌△DBM,∴AC=MD,∴欲求AC的最大值,只要求出DM的最大值即可.∵BC=4![]() =定值,∠BDC=90°,∴点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2
=定值,∠BDC=90°,∴点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2![]() +2
+2![]() ,∴AC的最大值为2
,∴AC的最大值为2![]() +2
+2![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.
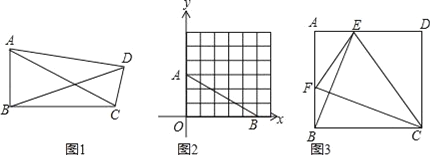
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
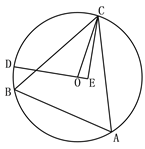
【题目】如图,△ABC为⊙O的内接三角形,BC=24 , ![]() ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
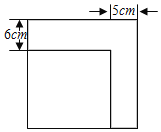
【题目】如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条.如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
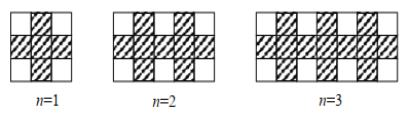
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:﹣32+|2﹣5|÷![]() +(﹣2)3×(﹣1)2015
+(﹣2)3×(﹣1)2015
(2)解方程:![]() ﹣
﹣![]() =3.
=3.
(3)解方程:6(x-2)=8x+3.
(4)解方程: x-![]() =2-
=2-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
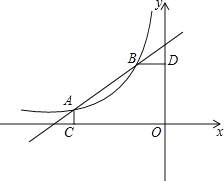
【题目】如图,在平面直角坐标系中,直线y=![]() x+
x+![]() 与反比例函数y=
与反比例函数y=![]() (x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(x<0)的图象交于A(-4,a)、B(-1,b)两点,AC⊥x轴于C,BD⊥y轴于D.
(1)求a 、b及k的值;
(2)连接OA,OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com