
【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.
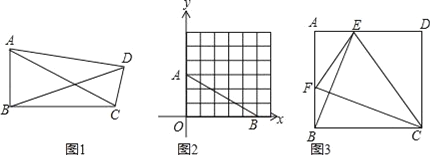
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
【答案】(1)![]() (2)(5,3),(3,5)(3)
(2)(5,3),(3,5)(3)![]() ;
;![]() ;
;![]()
【解析】试题分析:(1)利用准矩形的定义和勾股定理计算,再根据准矩形的特点和整点的特点求出即可;
(2)先利用正方形的性质判断出△ABE≌△BCF,即可;
(2)分三种情况分别计算,用到梯形面积公式,对角线面积公式,对角线互相垂直的四边形的面积计算方法.
试题解析:(1)①∵∠ABC=90,
∴BD=![]() ,
,
故答案为![]() ,
,
②∵A(0,3),B(5,0),
∴AB=![]() =6,
=6,
设点P(m,n),A(0,0),
∴OP=![]() =6,
=6,
∵m,n都为整数,
∴点P(3,5)或(5,3);
故答案为P(3,5)或(5,3);
(2)∵四边形ABCD是正方形,
∴AB=BC∠A=∠ABC=90°,
∴∠EAF+∠EBC=90°,
∵BE⊥CF,
∴∠EBC+∠BCF=90°,
∴∠EBF=∠BCF,
∴△ABE≌△BCF,
∴BE=CF,
∴四边形BCEF是准矩形;
(3)![]() ;
;![]() ;
;![]()
∵∠ABC=90°,∠BAC=60°,AB=2,
∴BC=2![]() ,AC=4,
,AC=4,
准矩形ABCD中,BD=AC=4,
①当AC=AD时,如图1,作DE⊥AB,
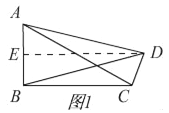
∴AE=BE![]() AB=1,
AB=1,
∴DE=![]() ,
,
∴S准矩形ABCD=S△ADE+S梯形BCDE
=![]() DE×AE+
DE×AE+![]() (BC+DE)×BE
(BC+DE)×BE
=![]() ×
×![]() +
+![]() (2
(2![]() +
+![]() )×1
)×1
=![]() +
+![]() ;
;
②当AC=CD时,如图2,

作DF⊥BC,
∴BD=CD,
∴BF=CF=![]() BC=
BC=![]() ,
,
∴DF=![]() ,
,
∴S准矩形ABCD=S△DCF+S梯形ABFD
=![]() FC×DF+
FC×DF+![]() (AB+DF)×BF
(AB+DF)×BF
=![]() ×
×![]() ×
×![]() +
+![]() (2+
(2+![]() )×
)×![]()
=![]() +
+![]() ;
;
③当AD=CD,如图3,
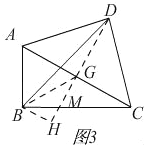
连接AC中点和D并延长,连接BG,过B作BH⊥DG,
∴BD=CD=AC=4,
∴AG=![]() AC=2,
AC=2,
∵AB=2,
∴AB=AG,
∵∠BAC=60°,
∴∠ABG=60°,
∴∠CBG=30°
在Rt△BHG中,BG=2,∠BGH=30°,
∴BH=1,
在Rt△BHM中,BH=1,∠CBH=30°,
∴BM=![]() ,HM=
,HM=![]() ,
,
∴CM=![]() ,
,
在Rt△DHB中,BH=1,BD=4,
∴DH=![]() ,∴DM=DH﹣MH=
,∴DM=DH﹣MH=![]() ﹣
﹣![]() ,
,
∴S准矩形ABCD=S△DCF+S四边形AMCD
=![]() BM×AB+
BM×AB+![]() AC×DM
AC×DM
=![]() ×
×![]() ×2+
×2+![]() ×4×(
×4×(![]() ﹣
﹣![]() )
)
=2![]() ;
;
故答案为![]() ;
;![]() ;
;![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠A=90°,AB=AC,∠ABC 的角平分线交 AC 于 D,BD=4 ![]() ,过点 C作 CE⊥BD 交 BD 的延长线于 E,则 CE 的长为( )
,过点 C作 CE⊥BD 交 BD 的延长线于 E,则 CE 的长为( )

A.![]() B.2
B.2 ![]() C.3
C.3 ![]() D.2
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,在
两点,在![]() 轴上有一点
轴上有一点![]() ,动点
,动点![]() 从
从![]() 点以每秒2个单位的速度沿
点以每秒2个单位的速度沿![]() 轴向左移动.
轴向左移动.
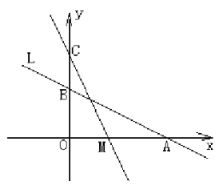
(1)求![]() 、
、![]() 两点的坐标
两点的坐标
(2)求![]() 的面积
的面积![]() 与
与![]() 的移动时间
的移动时间![]() (秒)之间的函数关系式;
(秒)之间的函数关系式;
(3)当![]() 何值时
何值时![]() ,并求此时
,并求此时![]() 点的坐标.
点的坐标.
(4)当![]() 何值时
何值时![]() 的面积是
的面积是![]() 一半,并求此时
一半,并求此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1 000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟.其中正确的说法是_________________(把你认为正确说法的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
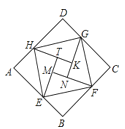
【题目】如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为![]() ,若
,若![]() ,则
,则![]() 的值是_______.
的值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.

(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,O为平面直角坐标系的原点,点的坐标分别为A(a,2)、B(a,-1),D(b,2).且a、b满足![]() .点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
.点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
(1)点C的坐标为_______________
(2)当点P移动在线段BC上时,求三角形ACP的面积(用含t的代数式表示)
(3)在移动过程中,当三角形ACP的面积是5时,直接写出点P移动的时间为几秒

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD、MN相交与点O,FO⊥BO,OM平分∠DOF
(1)请直接写出图中所有与∠AON互余的角: .
(2)若∠AOC=![]() ∠FOM,求∠MOD与∠AON的度数.
∠FOM,求∠MOD与∠AON的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com