
【题目】如图,在长方形ABCD中,O为平面直角坐标系的原点,点的坐标分别为A(a,2)、B(a,-1),D(b,2).且a、b满足![]() .点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
.点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
(1)点C的坐标为_______________
(2)当点P移动在线段BC上时,求三角形ACP的面积(用含t的代数式表示)
(3)在移动过程中,当三角形ACP的面积是5时,直接写出点P移动的时间为几秒

【答案】(1)![]() ;(2)
;(2)![]() ;(3)当三角形ACP的面积是5时,
;(3)当三角形ACP的面积是5时,![]() 、
、![]() 、
、![]() .
.
【解析】
(1)根据![]() 可得到
可得到![]() ,
,![]() ,由矩形的性质可得C点的横坐标与D点的相等,纵坐标与B点相同,即可得到结论;
,由矩形的性质可得C点的横坐标与D点的相等,纵坐标与B点相同,即可得到结论;
(2)因为点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,且当点P移动在线段BC上时,可得BP=t,根据三角形面积公式即可得到结果;
(3)分类讨论,当P在AB上运动和BC上运动进行讨论;
(1)根据![]() 可得:
可得:
![]() 和
和![]() ,
,
解得![]() ,
,![]() ,
,
∴A(2,2)、B(2,-1),D(-4,2),
∵四边形ABCD是矩形,
∴C的横坐标坐标-4,纵坐标为-1,
∴![]() .
.
(2)由题可知BP=t,
由(1)可知,AB=3,BC=6,且点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,
∴当t=3时,P点运动到点B,当t=9时,点P运动到C处,
根据图形可得△ACP的面积=![]() ,
,
∵BP=t-3,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故![]() .
.
(3)当点P在AB边上运动时,
![]() ,
,
当角形ACP的面积是5时,可得![]() ,
,
解得![]() ;
;
当点P在AB边上运动时,
由(1)得![]() ,
,
当角形ACP的面积是5时,可得![]() ,
,
解得:![]() ,
,
当点P在CD上运动时,![]() ,
,
![]()
当角形ACP的面积是5时,可得![]() ,
,
解得:![]() ;
;
当点P在DA上运动时,![]() ,
,
∴DP=t-12,
∴AP=18-(t-12)=30-t,
![]() ,
,
当角形ACP的面积是5时,可得![]() ,
,
解得:![]() (舍去);
(舍去);
故当三角形ACP的面积是5时,![]() 、
、![]() 、
、![]() .
.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.
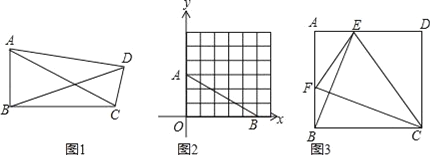
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一,在平面里有两点![]() ,
,![]() ,若
,若![]() 为起点,
为起点,![]() 为终点,则把有方向且有长度的线段
为终点,则把有方向且有长度的线段![]() 叫做向量,记为:
叫做向量,记为:![]() ,并且可用坐标表示这个向量,表示方法为:
,并且可用坐标表示这个向量,表示方法为:
![]() ,向量
,向量![]() 的长度可以表示成
的长度可以表示成![]()
例如:![]() ,
,![]() 则
则![]() ,
,
即![]() 所以
所以![]()
材料二:若![]() ,
,![]() ,则
,则![]()
若![]() 时,则
时,则![]() .
.
根据材料解决下列问题:
已知![]() 中,
中,![]() ,
,![]() ,
,![]()
(1)![]() ________
________ ![]() ___________
___________
(2)当![]() 时,求证:
时,求证:![]() 是直角三角形.
是直角三角形.
(3)若![]() ,
,![]() ,求使
,求使![]() 恒成立的
恒成立的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点是法国数学家和教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副三角板的直角重合放置,其中∠A=30°,∠CDE=45°.

(1)如图1,求∠EFB的度数;
(2)若三角板ACB的位置保持不动,将三角板CDE绕其直角顶点C顺时针方向旋转.
①当旋转至如图2所示位置时,恰好CD∥AB,则∠ECB的度数为 ;
②若将三角板CDE继续绕点C旋转,直至回到图1位置.在这一过程中,是否还会存在△CDE其中一边与AB平行?如果存在,请你画出示意图,并直接写出相应的∠ECB的大小;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com