Question

【题目】如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．

（1）求证：BC是⊙O的切线；
（2）若⊙O的半径为3，OP=1，求BC的长．

Answer 1

【答案】
（1）证明：连接OB，如图，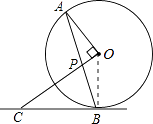

∵OP⊥OA，
∴∠AOP=90°，
∴∠A+∠APO=90°，
∵CP=CB，
∴∠CBP=∠CPB，
而∠CPB=∠APO，
∴∠APO=∠CBP，
∵OA=OB，
∴∠A=∠OBA，
∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°，
∴OB⊥BC，
∴BC是⊙O的切线
（2）解：设BC=x，则PC=x，
在Rt△OBC中，OB=3，OC=CP+OP=x+1，
∵OB2+BC2=OC2 ，
∴32+x2=（x+1）2 ，
解得x=4，
即BC的长为4
【解析】（1）要证明BC是⊙O的切线，连半径证垂直，因此连接OB，先根据垂线的定义及三角形内角和定理证明∠A+∠APO=90°，再根据对顶角相等及等腰三角形的性质证明∠APO=∠CBP，∠CBP=∠CPB，∠A=∠OBA，然后再证明∠OBC=90°，即可证得结论。
（2）根据已知设CP=CB=x，用含x的代数式表示出OC，再在Rt△OBC中，利用勾股定理建立关于x的方程，解方程求出x的值，即可得出答案。