【题目】如图，直线DE经过点A．
（1）写出∠B的内错角是 ，同旁内角是 ．
（2）若∠EAC＝∠C，AC平分∠BAE，∠B＝44°，求∠C的度数．
【答案】（1）∠BAD；∠BAC，∠EAB和∠C；（2）68°．
【解析】
（1）根据内错角和同旁内角的概念解答即可；（2）根据平行线的判定和性质解答即可．
解：（1）∠B的内错角是∠BAD，是
与
被
所截形成的内错角，
∠B的同旁内角是∠BAC，是与
被所截形成的同旁内角，
∠B的同旁内角是∠EAB，是与被所截形成的同旁内角，
∠B的同旁内角是∠C，是与被所截形成的同旁内角，
故答案为：∠B的内错角是∠BAD，∠B的同旁内角是∠BAC，∠EAB和∠C；
（2）∵∠EAC＝∠C，
∴DE∥BC，
∴∠BAE＝180°﹣44°＝136°，
∵AC平分∠BAE，
∴∠EAC＝68°，
∴∠C＝∠EAC＝68°，
科目：初中数学 来源： 题型：
【题目】如图，在长方形ABCD中，O为平面直角坐标系的原点，点的坐标分别为A(a，2)、B(a，-1)，D(b，2)．且a、b满足
．点P从A点出发，以每秒1个单位长度的速度A-B-C-D-A的线路移动，运动时间为t，当点P回到A点时运动停止
（1）点C的坐标为_______________
（2）当点P移动在线段BC上时，求三角形ACP的面积（用含t的代数式表示）
（3）在移动过程中，当三角形ACP的面积是5时，直接写出点P移动的时间为几秒
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知两直线L1：y=k1x+b1 ， L2：y=k2x+b2 ， 若L1⊥L2 ， 则有k1k2=﹣1．
（1）应用：已知y=2x+1与y=kx﹣1垂直，求k；
（2）直线经过A（2，3），且与y= 
x+3垂直，求解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AB是⊙O的直径，C、E是⊙O上的点， CD⊥AB，EF⊥AB，垂足分别为D、F，过点E作 EG⊥0C，垂足为G，延长EG交OA于H。
求证：
（1）HO·HF=HG·HE；
（2）FG=CD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在锐角△ABC中，∠BAC＝60，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①DF＝EF；②AD∶AB＝AE∶AC；③△DEF是等边三角形；④BE＋CD＝BC；⑤当∠ABC＝45时，BE＝
DE中，一定正确的有 ．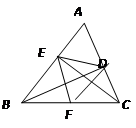 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
