练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知两直线L1：y=k1x+b1 ， L2：y=k2x+b2 ， 若L1⊥L2 ， 则有k1k2=﹣1．
    （1）应用：已知y=2x+1与y=kx﹣1垂直，求k；
    （2）直线经过A（2，3），且与y= x+3垂直，求解析式．

    【答案】
    （1）解：∵L1⊥L2，则k1k2=﹣1，

    ∴2k=﹣1，

    ∴k=﹣


    （2）解：∵过点A直线与y= x+3垂直，

    ∴设过点A直线的直线解析式为y=3x+b，

    把A（2，3）代入得，b=﹣3，

    ∴解析式为y=3x﹣3


    【解析】（1）根据已知两直线L1，L2若L1⊥L2，则有k1k2=﹣1．建立方程2k=-1，求解即可，
    （2）根据k1k2=﹣1，可设函数解析式为y=3x+b，将点A的坐标代入，即可求出函数解析式。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人在某标准游泳池相邻泳道进行100米自由泳训练，如图是他们各自离出发点的距离y（米）与他们出发的时间x（秒）的函数图象．根据图象，解决如下问题．（注标准泳池单向泳道长50米，100米自由泳要求运动员在比赛中往返一次；返回时触壁转身的时间，本题忽略不计）.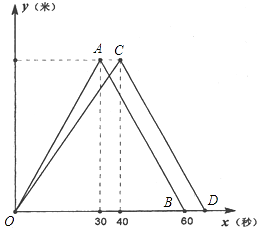

    （1）直接写出点A坐标，并求出线段OC的解析式；
    （2）他们何时相遇？相遇时距离出发点多远？
    （3）若甲、乙两人在各自游完50米后，返回时的速度相等；则快者到达终点时领先慢者多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a>0，b<0，则点(a，b1)在（ ）

    A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在锐角三角形中，∠A>∠B>∠C，则下列结论中错误的是（ ）

    A. ∠A>60° B. ∠B>45° C. ∠C<60° D. ∠B+∠C<90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中：①线段是轴对称图形，②成轴对称的两个图形对称点的连线互相平行，③等腰三角形的角平分线就是底边的垂直平分线，④已知两腰就能确定等腰三角形的形状和大小，正确的有( ) ．

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a=－2×32，b=(－2×3)2，c=－(2×3)2，将a，b，c三个数用“＜”连接起来应为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，O为原点，直线l：x=1，点A（2，0），点E，点F，点M都在直线l上，且点E和点F关于点M对称，直线EA与直线OF交于点P．
    （Ⅰ）若点M的坐标为（1，﹣1），
    ①当点F的坐标为（1，1）时，如图，求点P的坐标；
    ②当点F为直线l上的动点时，记点P（x，y），求y关于x的函数解析式．
    （Ⅱ）若点M（1，m），点F（1，t），其中t≠0，过点P作PQ⊥l于点Q，当OQ=PQ时，试用含t的式子表示m．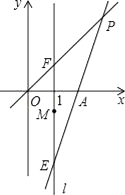

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】《函数的图象与性质》拓展学习片段展示：

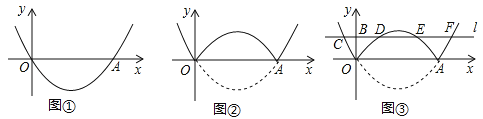
    【问题】如图①，在平面直角坐标系中，抛物线y=a（x﹣2）2﹣经过原点O，与x轴的另一个交点为A，则a= ．

    【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G，如图②．直接写出图象G对应的函数解析式．

    【探究】在图②中，过点B（0，1）作直线l平行于x轴，与图象G的交点从左至右依次为点C，D，E，F，如图③．求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围．

    【应用】P是图③中图象G上一点，其横坐标为m，连接PD，PE．直接写出△PDE的面积不小于1时m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系XOY中，A（-1，5），B（-1，0），C（-4，3）．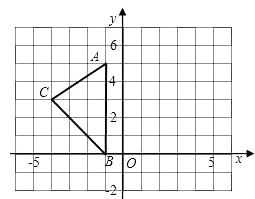

    （1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
    （2）直接写出A′，B′，C′三点的坐标：A′（ ），B′（ ），C′（ ）
    （3）计算△ABC的面积．

    查看答案和解析>>

    同步练习册答案