
【题目】甲、乙两人在某标准游泳池相邻泳道进行100米自由泳训练,如图是他们各自离出发点的距离y(米)与他们出发的时间x(秒)的函数图象.根据图象,解决如下问题.(注标准泳池单向泳道长50米,100米自由泳要求运动员在比赛中往返一次;返回时触壁转身的时间,本题忽略不计).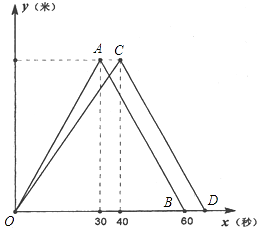
(1)直接写出点A坐标,并求出线段OC的解析式;
(2)他们何时相遇?相遇时距离出发点多远?
(3)若甲、乙两人在各自游完50米后,返回时的速度相等;则快者到达终点时领先慢者多少米?
【答案】
(1)解:由图得点A(30,50),C(40,50),
设线段OC的解析式为:y1=k1x,
把点C(40,50)代入得, ![]() ,
,
∴线段OC的解析式为:y1= ![]() (0≤x≤40)
(0≤x≤40)
(2)解:设线段AB的解析式为y2=k2x+b,
把点A(30,50)、点B(60,0)代入可知: ![]()
解得, 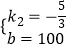 ,
,
∴线段AB的解析式为y2= ![]() ,(30≤x≤60);
,(30≤x≤60);
解方程组 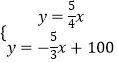 ,
,
解得, 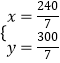 ,∴线段OC与线段AB的交点为(
,∴线段OC与线段AB的交点为( ![]() ,
, ![]() ),
),
即出发 ![]() 秒后相遇,相遇时距离出发点
秒后相遇,相遇时距离出发点 ![]() 米
米
(3)解:∵甲乙两人在各自游完50米后,在返程中的距离保持不变,
把x=30代入y1= ![]() ,得y1=
,得y1= ![]() 米,
米,
把x=40代入y2= ![]() ,得y2=
,得y2= ![]() 米,
米,
∴快者到达终点时,领先慢者 ![]() 米
米
【解析】 (1)观察图像易得出点A的坐标,线段OC是正比例函数,设函数解析式,再将点C的坐标代入即可得出结果。
(2)先根据点A、B的坐标求出直线AB的函数解析式,再将直线AB和直线CD联立方程组,解方程组,即可得出两直线的交点坐标,根据交点坐标即可得出结果。
(3)将x=30和x=40分别代入y1和y2,即可求出快者到达终点时,领先慢者的路程。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题为真命题的是( )
A.和为180°的两个角是邻补角B.内错角相等
C.经过直线外一点有且只有一条直线与这条直线平行D.同旁内角相等,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把长方形 ![]() 沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,
沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,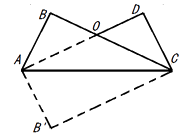
(1)求∠AOC和∠BAC的度数;
(2)若AD= ![]() ,OD=
,OD= ![]() ,求CD的长
,求CD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号1,2,3,4,5的五位同学最后成绩如表所示:那么这五位同学演讲成绩的众数与中位数依次是( )
参赛者编号 | 1 | 2 | 3 | 4 | 5 |
成绩/分 | 96 | 88 | 86 | 93 | 86 |
A.96,88
B.86,88
C.88,86
D.86,86
查看答案和解析>>
科目:初中数学 来源: 题型:
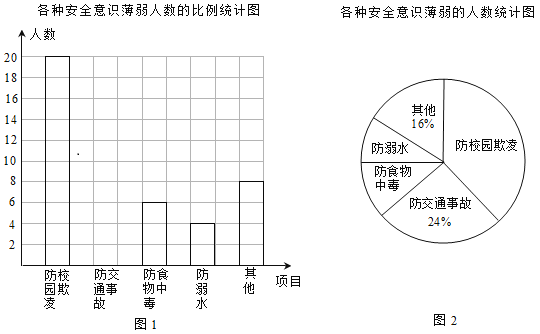
【题目】某校组织了一次防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识的调查活动,了解同学们在哪些方面的安全意识薄弱,便于今后更好地开展安全教育活动.根据调查结果,绘制出图1,图2两幅不完整的统计图.
请结合图中的信息解答下列问题:
(1)本次调查的人数为___________,其中防校园欺凌意识薄弱的人数占_________%;
(2)补全条形统计图;
(3)若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数;
(4)请你根据题中的信息,给该校的安全教育提一个合理的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线L1:y=k1x+b1 , L2:y=k2x+b2 , 若L1⊥L2 , 则有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y= ![]() x+3垂直,求解析式.
x+3垂直,求解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com