
【题目】已知AB是⊙O的直径,C、E是⊙O上的点, CD⊥AB,EF⊥AB,垂足分别为D、F,过点E作 EG⊥0C,垂足为G,延长EG交OA于H。
求证:
(1)HO·HF=HG·HE;
(2)FG=CD
【答案】
(1)解:证明:∵ EG⊥0C, EF⊥AB
∴ ∠HGO=∠HFE=90°
又 ∵ ∠GHO=∠FHE
∴△HGO∽△HFE
∴ ![]()
即HO·HF=HG·HE 。
(2)解:过点G作 GM⊥0H,垂足为M,连结OE 
∵ ![]() ,∠EHO=∠FHG
,∠EHO=∠FHG
∴ △HGF∽△HOE
∴ ∠HFG=∠HEO
∵ GM⊥0H,EG⊥0C
∴∠GMF=∠OGE=90°
∴ Rt△FGM∽Rt△EOG
∴ ![]()
又 GM∥CD
∴ ![]() 即
即 ![]()
∴ ![]() 由OE=OC,得GF=CD 。
由OE=OC,得GF=CD 。
【解析】(1)根据垂直的定义得出 ∠HGO=∠HFE=90°,又 ∠GHO=∠FHE ,从而判断出 △HGO∽△HFE ,根据相似三角形对应边成比例得出![]() 根据比例的性质得出 HO·HF=HG·HE;
根据比例的性质得出 HO·HF=HG·HE;
(2)过点G作 GM⊥0H,垂足为M,连结OE ,根据![]() 及∠EHO=∠FHG由两边对应成比例,及夹角相等的两个三角形相似得出△HGF∽△HOE,由相似三角形对应角相等得出 ∠HFG=∠HEO ,根据垂直的定义得出∠GMF=∠OGE=90°,进而得出 Rt△FGM∽Rt△EOG;由相似三角形对应边成比例得出
及∠EHO=∠FHG由两边对应成比例,及夹角相等的两个三角形相似得出△HGF∽△HOE,由相似三角形对应角相等得出 ∠HFG=∠HEO ,根据垂直的定义得出∠GMF=∠OGE=90°,进而得出 Rt△FGM∽Rt△EOG;由相似三角形对应边成比例得出![]() ,根据平行线分线段成比例定理得出
,根据平行线分线段成比例定理得出![]() ,即
,即![]() ,进而得出
,进而得出![]() ,根据OE=OC,得GF=CD。
,根据OE=OC,得GF=CD。


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】(1) 发现:
如图1,点![]() 是线段
是线段![]() 外一动点,且
外一动点,且![]() ,
,![]() .当点
.当点![]() 位于 时,线段
位于 时,线段![]() 的长取得最大值;最大值为 (用含
的长取得最大值;最大值为 (用含![]() ,
,![]() 的式子表示).
的式子表示).

(2)应用:
如图2,点![]() 为线段
为线段![]() 外一动点,
外一动点,![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 为边在
为边在![]() 外部作等边
外部作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,
,![]() .
.
①求证:![]() ;
;
②直接写出线段![]() 长的最大值.
长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() 为线段
为线段![]() 外一动点,
外一动点,![]() ,
,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 长的最大值及此时点
长的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点是法国数学家和教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c+2的图象如图,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )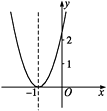
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年宜宾市创建全国文明城市的过程中,某小区决定购买文明用语提示牌和文明信息公示栏.若购买2个提示牌和3个公示栏需要510元;购买3个提示牌和5个公示栏需要840元.
(1)求提示牌和公示栏的单价各是多少元?
(2)若该小区购买提示牌和公示栏共50个,要求购买公示栏至少12个,且总费用不超过3200元.请你列举出所有购买方案,并指出哪种方案费用最少,最少费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两点在数轴上如图所示,其中O为原点,点A对应的有理数为a,点B对应的有理数为b,且点A距离原点6个单位长度,a.b满足b-|a|=2.
(1)a=______;b=______;
(2)动点P从点A出发,以每秒2个单位长度的速度向右运动,设运动时间为t秒(t>0)
①当PO=2PB时,求点P的运动时间t:
②当PB=6时,求t的值:
(3)当点P运动到线段OB上时,分别取AP和OB的中点E、F,则![]() 的值是否为一个定值?如果是,求出定值,如果不是,说明理由.
的值是否为一个定值?如果是,求出定值,如果不是,说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com