
【题目】为了运送防疫物资,甲、乙两货运公司各派出一辆卡车,分别从距目的地240千米和270千米的两地同时出发,驰援疫区.已知乙公司卡车的平均速度是甲公司卡车的平均速度的1.5倍,甲公司的卡车比乙公司的卡车晚1小时到达目的地,分别求甲、乙两货运公司卡车的平均速度.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
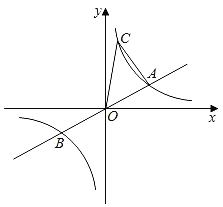
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,A点的横坐标为3,则下列结论:①k=6;②A点与B点关于原点O中心对称;③关于x的不等式
(k>0)交于A、B两点,A点的横坐标为3,则下列结论:①k=6;②A点与B点关于原点O中心对称;③关于x的不等式![]() <0的解集为x<﹣3或0<x<3;④若双曲线y=
<0的解集为x<﹣3或0<x<3;④若双曲线y=![]() (k>0)上有一点C的纵坐标为6,则△AOC的面积为8,其中正确结论的个数( )
(k>0)上有一点C的纵坐标为6,则△AOC的面积为8,其中正确结论的个数( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(发现证明)
如图1,在正方形ABCD中,点E,F分别是BC,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.

小明发现,当把△ABE绕点A顺时针旋转90°至△ADG,使AB与AD重合时能够证明,请你给出证明过程.
(2)(类比引申)①如图2,在正方形ABCD中,如果点E,F分别是CB,DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.
②如图3,如果点E,F分别是BC,CD延长线上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是 (不要求证明)
(3)(联想拓展)如图1,若正方形ABCD的边长为6,AE=3![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是______________.(填序号)
;④0<CE≤6.4.其中正确的结论是______________.(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).

(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
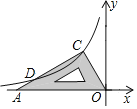
【题目】如图,把一块含30°角的三角板的直角顶点放在反比例函数y=-![]() (x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标为__________.
(x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上一点(不与点A、B重合),D是![]() 的中点,DE⊥AB于点E,过点C作半圆O的切线,交ED的延长线于点F.
的中点,DE⊥AB于点E,过点C作半圆O的切线,交ED的延长线于点F.
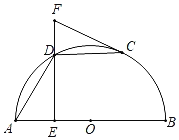
(1)求证:∠FCD=∠ADE;
(2)填空:
①当∠FCD的度数为 时,四边形OADC是菱形;
②若AB=2![]() ,当CF∥AB时,DF的长为 .
,当CF∥AB时,DF的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com