
【题目】如图,点![]() 在双曲线
在双曲线![]() 上,连接
上,连接![]() ,分别以点
,分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() 两点,直线
两点,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .若
.若![]() ,则
,则![]() 的值为___.
的值为___.

【答案】![]()
【解析】
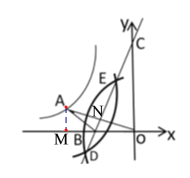
过点A作AM⊥x轴于点M,设AO与BC交于点N,易证![]() ,得
,得![]() ,设AM=a,可得:MO=3a,由勾股定理,列出关于a的方程,求出a的值,进而的点A的坐标,即可求解.
,设AM=a,可得:MO=3a,由勾股定理,列出关于a的方程,求出a的值,进而的点A的坐标,即可求解.
过点A作AM⊥x轴于点M,设AO与BC交于点N,
∵由作图可知:BC垂直平分AO,
∴∠AOM+∠CON=∠CON+∠DCO=90°,![]() ,
,
∴∠AOM=∠DCO,
∵∠AMO=∠BOC=90°,
∴![]() ,
,
∴![]() ,
,
设AM=a,
∴![]() ,即:MO=3a,
,即:MO=3a,
∴BM=3a-1,
∵在Rt![]() ABM中,AB2=AM2+BM2,
ABM中,AB2=AM2+BM2,
∴12=a2+(3a-1)2,解得:![]() (舍去),
(舍去),
∴AM=![]() ,MO=
,MO=![]() ,
,
∴A(-![]() ,
,![]() ),
),
∵点![]() 在双曲线
在双曲线![]() 上,
上,
∴k=(-![]() )×
)×![]() =
=![]() .
.
故答案是:![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
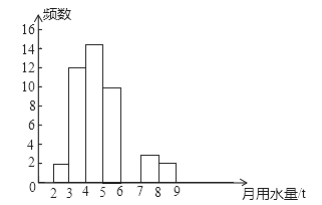
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF; ②点E到AB的距离是2![]() ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为(0,2)、(1,0),顶点C在函数y=![]() x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了运送防疫物资,甲、乙两货运公司各派出一辆卡车,分别从距目的地240千米和270千米的两地同时出发,驰援疫区.已知乙公司卡车的平均速度是甲公司卡车的平均速度的1.5倍,甲公司的卡车比乙公司的卡车晚1小时到达目的地,分别求甲、乙两货运公司卡车的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com