
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为(0,2)、(1,0),顶点C在函数y=![]() x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x (时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:喝酒后几时血液中的酒精含量达到最大值?最大值为多少
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:30在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】育红学校七年级学生步行到郊外旅行.七(1)班的学生组成前队,步行速度为4km/h,七(2)班的学生组成后队,速度为6km/h.前队出发1h后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.
(1)当联络员追上前队时,离出发点多远?
(2)当联络员追上前队再到后队集合,总共用了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.
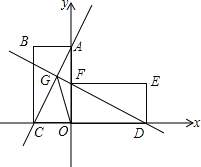
(1)求直线DF的解析式;
(2)求证:GO平分∠CGD;
(3)在角平分线GO上找一点M,使以点G、M、D为顶点的三角形是等腰直角三角形,求出M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
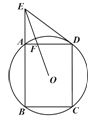
【题目】如图,矩形ABCD接于半径为2.5的⊙O,AB=4, 延长BA到E,使AE=![]() ,连接ED.
,连接ED.
(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于F,求FO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
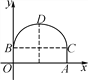
【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12 m,宽OB为4 m,隧道顶端D到路面的距离为10 m,建立如图所示的直角坐标系.
(1)求该抛物线的表达式;
(2)一辆货车载有一个长方体集装箱,集装箱最高处与地面距离为6 m,宽为4 m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排离地面高度相等的灯,如果灯离地面的高度不超过8.5 m,那么这两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数![]() ,
,![]() 表示的点在数轴上的位置如图所示.
表示的点在数轴上的位置如图所示.
![]()
(1)在数轴上表示出![]() ,
,![]() 的相反数的位置;
的相反数的位置;
(2)若数![]() 与其相反数相距20个单位长度,则
与其相反数相距20个单位长度,则![]() 表示的数是多少?
表示的数是多少?
(3)在(2)的条件下,若数![]() 表示的点与数
表示的点与数![]() 的相反数表示的点相距5个单位长度,求
的相反数表示的点相距5个单位长度,求![]() 表示的数是多少?
表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com