
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

【答案】见解析;2.
【解析】试题分析:根据正方形的性质得到AD=AB,∠B=∠D=90°,根据折叠的性质可得AD=AF,∠AFE=∠D=90°,从而得到∠AFG=∠B=90°,AB=AF,结合AG=AG得到三角形全等;根据全等得到BG=FG,设BG=FG=x,则CG=6-x,根据E为中点得到CE=EF=DE=3,则EG=3+x,根据Rt△ECG的勾股定理得出x的值.
试题解析:(1)、∵四边形ABCD是正方形,∴∠B=∠D=90°,AD=AB,由折叠的性质可知
AD=AF,∠AFE=∠D=90°, ∴∠AFG=90°,AB=AF, ∴∠AFG=∠B, 又AG=AG, ∴△ABG≌△AFG;
(2)、∵△ABG≌△AFG, ∴BG=FG, 设BG=FG= ![]() ,则GC=
,则GC= ![]() , ∵E为CD的中点,
, ∵E为CD的中点,
∴CE=EF=DE=3, ∴EG= ![]() , ∴
, ∴![]() , 解得
, 解得![]() , ∴BG=2.
, ∴BG=2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(﹣1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )
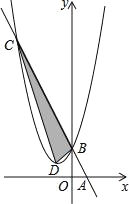
A.8:1 B.6:1 C.5:1 D.4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个点中在函数y=2x-3的图象上有( )个.
(1,2) , (3,3) , (-1, -1), (1.5,0)
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连接CD.
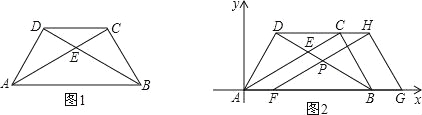
(1)填空:如图1,AC的长度= ,tan∠ABD= ;
(2)试判断△ADC与△AEB的关系,并说明理由;
(3)如图2建立平面直角坐标系,保持△ABD不动,将△ABC向x轴的正方向平移到△FGH的位置,FH与BD相交于点P,设AF=t,△FBP面积为S,求S与t之间的函数关系式,并写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com