
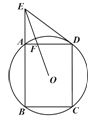
【题目】如图,矩形ABCD接于半径为2.5的⊙O,AB=4, 延长BA到E,使AE=![]() ,连接ED.
,连接ED.
(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于F,求FO的长.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)连结BD.由ABCD是矩形,得到BD的长.在Rt△ABD中,由勾股定理得到AD的长.在Rt△AED中,由勾股定理得到ED2.在△BED中,由勾股定理得到BE2,从而得到BD2=BE2-ED2,由勾股定理的逆定理得到∠BDE=90°,从而得到结论.
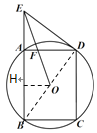
(2)过点O作OH⊥AB于H,由垂径定理得到AH=BH=2.由三角形中位线定理得到OH=![]() AD=1.5.在Rt△EHO中,由勾股定理得到EO的长.再由OH∥AD,得到
AD=1.5.在Rt△EHO中,由勾股定理得到EO的长.再由OH∥AD,得到![]() ,从而得到结论.
,从而得到结论.
详解:(1)连结BD.
∵ABCD是矩形,∴∠BAD=90°,∴BD是直径,∴BD=5.
在Rt△ABD中,AD=![]() =3,
=3,
∠EAD=180°-∠BAD=90°.
在Rt△AED中,ED2=AD2+AE2=![]() .
.
在△BED中,BE2=(4+![]() )2=
)2=![]() ,BD2=25,BE2-ED2=
,BD2=25,BE2-ED2=![]() -
-![]() =25,
=25,
∴BD2=BE2-ED2,∴∠BDE=90°.
又∵BD是直径,∴ED是⊙O的切线.
(2)过点O作OH⊥AB于H,则AH=BH=![]() AB=2.
AB=2.
又∵OB=OD,∴OH=![]() AD=1.5.
AD=1.5.
在Rt△EHO中,EO=![]() =
=![]() .
.
∵∠OHB=∠DAB=90°,∴OH∥AD.
∴![]() .
.
∴OF=![]() .
.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
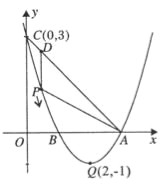
【题目】如图,已知抛物线![]() 的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
【1】求该抛物线的函数关系式;
【1】求点P在运动的过程中,线段PD的最大值;
【1】当△ADP是直角三角形时,求点P的坐标;
【1】在题(3)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B在数轴上对应的数分别用a、b表示,且(a-20)2+|b+10|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离;
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数;
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,…….点P能移动到与A或B重合的位置吗?若不能,请直接回答;若能,请直接指出,第几次移动,与哪一点重合.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,正中设计一个圆形喷水池,若四周圆形和中间圆形的半径均为![]() 米,广场长为
米,广场长为![]() 米,宽为
米,宽为![]() 米.
米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为400米,宽为300米,圆形花坛的半径为20米,求广场空地的面积(计算结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为(0,2)、(1,0),顶点C在函数y=![]() x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明元旦节吃完晚饭后6点过还没到7点,他陪他妈到成华区SM广场去买东西,离家时他发现他家的时钟上时针与分针刚好重合,他离家的时间是_______(用几点几分几秒表示,注意“四舍五入”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是边长为![]() 的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1,B1C1交BC于点D,B1C1交AC于点E,则CE=( )
的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1,B1C1交BC于点D,B1C1交AC于点E,则CE=( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按如图方式拼图,第1个图形共用3根火柴棒,第2个图形共用9根火柴棒,第3个图形共用18根火柴棒,……按照这样的方式继续拼图,第n个图形共用_____根火柴棒.(用含n的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com