
【题目】已知,A、B在数轴上对应的数分别用a、b表示,且(a-20)2+|b+10|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离;
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数;
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,…….点P能移动到与A或B重合的位置吗?若不能,请直接回答;若能,请直接指出,第几次移动,与哪一点重合.
![]()
【答案】(1)数轴见解析,30;(2)P点对应的数为-6或2.(3)第20次P与A重合.
【解析】
(1)先根据非负数的性质求出a,b的值,在数轴上表示出A、B的位置,根据数轴上两点间的距离公式,求出A、B之间的距离即可;
(2)设P点对应的数为x,当P点满足PB=2PC时,分三种情况讨论,根据PB=2PC求出x的值即可;
(3)根据第一次点P表示-1,第二次点P表示2,点P表示的数依次为-3,4,-5,6…,找出规律即可得出结论.
(1)∵(a-20)2+|b+10|=0,
∴a=20,b=-10,
∴AB=20-(-10)=30,
数轴上标出A、B得:
![]()
(2)∵|BC|=6且C在线段OB上,
∴xC-(-10)=6,
∴xC=-4,
∵PB=2PC,
当P在点B左侧时PB<PC,此种情况不成立,
当P在线段BC上时,
xP-xB=2(xc-xp),
∴xp+10=2(-4-xp),
解得:xp=-6;
当P在点C右侧时,
xp-xB=2(xp-xc),
xp+10=2xp+8,
xp=2.
综上所述P点对应的数为-6或2.
(3)第一次点P表示-1,第二次点P表示2,依次-3,4,-5,6…
则第n次为(-1)nn,
点A表示20,则第20次P与A重合;
点B表示-10,点P与点B不重合.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
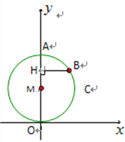
【题目】如图8,在平面直角坐标系中,点A坐标为(0,3),点B(![]() ,
,![]() )是以OA为直径的⊙M上的一点,且tan∠AOB=
)是以OA为直径的⊙M上的一点,且tan∠AOB=![]() ,BH⊥
,BH⊥![]() 轴,H为垂足,点C(
轴,H为垂足,点C(![]() ,
,![]() ).
).
(1)求H点的坐标;
(2)求直线BC的解析式;
(3)直线BC是否与⊙M相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM,ON分别为∠AOC,∠AOB的平分线.

(1)∠COD与∠AOB相等吗?请说明理由;
(2)若∠AOB=30°,试求∠AOM与∠MON的度数;
(3)若∠MON=42°,试求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
a | a+2 | a+4 | … |
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?若这间阶梯教室共有15排,那么最多可容纳多少学员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】育红学校七年级学生步行到郊外旅行.七(1)班的学生组成前队,步行速度为4km/h,七(2)班的学生组成后队,速度为6km/h.前队出发1h后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.
(1)当联络员追上前队时,离出发点多远?
(2)当联络员追上前队再到后队集合,总共用了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.
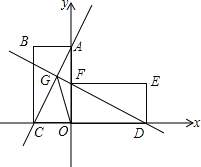
(1)求直线DF的解析式;
(2)求证:GO平分∠CGD;
(3)在角平分线GO上找一点M,使以点G、M、D为顶点的三角形是等腰直角三角形,求出M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
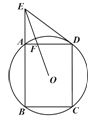
【题目】如图,矩形ABCD接于半径为2.5的⊙O,AB=4, 延长BA到E,使AE=![]() ,连接ED.
,连接ED.
(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于F,求FO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com