
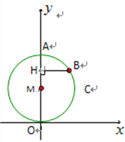
【题目】如图8,在平面直角坐标系中,点A坐标为(0,3),点B(![]() ,
,![]() )是以OA为直径的⊙M上的一点,且tan∠AOB=
)是以OA为直径的⊙M上的一点,且tan∠AOB=![]() ,BH⊥
,BH⊥![]() 轴,H为垂足,点C(
轴,H为垂足,点C(![]() ,
,![]() ).
).
(1)求H点的坐标;
(2)求直线BC的解析式;
(3)直线BC是否与⊙M相切?请说明理由.
【答案】(1) H(0,![]() ); (2)
); (2) ![]() =-
=-![]()
![]() +4;(3)见解析.
+4;(3)见解析.
【解析】分析:
(1)由已知易得tan∠AOB=![]() ,BH=
,BH=![]() ,由此即可解得m=
,由此即可解得m=![]() ,从而可得点H的坐标;
,从而可得点H的坐标;
(2)由(1)可知点B的坐标为![]() 结合点C的坐标即可由待定系数法求得直线BC的解析式;
结合点C的坐标即可由待定系数法求得直线BC的解析式;
(3)设直线BC与两坐标轴的交点分别为E、F,由(2)中所得解析式可求得点E、F的坐标,过点M作MN⊥BC于点N,由S△FME=![]() EF·MN=
EF·MN=![]() FM·EO,可证得MN的长等于⊙M的半径,由此即可得到BC是⊙M的切线.
FM·EO,可证得MN的长等于⊙M的半径,由此即可得到BC是⊙M的切线.
详解:
(1)由tan∠AOB=![]() ,得
,得![]() =
=![]() ,
,
∴OH=2BH,又B(![]() ,
,![]() ),即
),即![]() =2×
=2×![]() =
=![]() ,
,
∴H点的坐标为H(0,![]() );
);
(2)设过点B(![]() ,
,![]() )及点C(
)及点C(![]() ,
,![]() )
)
的直线解析式为:![]() =
=![]() +
+![]() ,
,
把BC坐标分别代入,得: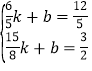 ,
,
解得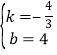 ,
,
∴直线BC的解析式为:![]() =-
=-![]()
![]() +4;
+4;
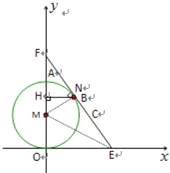
(3)BC与⊙M相切,理由如下
如下图,设直线BC:![]() 分别与
分别与![]() 轴
轴![]() 轴交于点EF,
轴交于点EF,
则点E的坐标为(3,0)点F的坐标为(0,4),
∴OE=3,OF=4,
∴EF=5,
过圆心M作MN⊥EF,垂足为N,连结ME,
∵S△FME=![]() EF·MN=
EF·MN=![]() FM·EO,
FM·EO,
∴得EF·MN=FM·EO,
∵⊙M的直径为3,
∴⊙M的半径OM=1.5,
∴MF=4-1.5=2.5,
∴MN=![]() =
=![]() ,
,
即圆心M到直线BC的距离等于⊙M的半径,
∴直线BC是⊙M的切线.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)(单位:万人),其中9月30日的游客人数为2万:

(1)请问10月2日的游客人数为多少?
(2)请判断7天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(3)求这一次黄金周期间该风景区游客总人数.(假设每天游客都不重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.

(1)过点C画线段AB的平行线CD;
(2)过点A画线段BC的垂线,垂足为E;
(3)线段AE的长度是点 到直线 的距离;
(4)比较线段AE、AB、BC的大小关系(用“<”连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
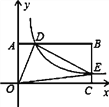
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=( )
A. 6 B. 9 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(5分)某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负):

⑴根据记录可知前三天共生产________辆;
⑵产量最多的一天比产量最少的一天多生产________辆;
⑶该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
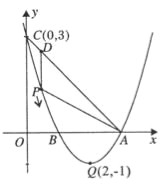
【题目】如图,已知抛物线![]() 的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
【1】求该抛物线的函数关系式;
【1】求点P在运动的过程中,线段PD的最大值;
【1】当△ADP是直角三角形时,求点P的坐标;
【1】在题(3)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B在数轴上对应的数分别用a、b表示,且(a-20)2+|b+10|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离;
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数;
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,…….点P能移动到与A或B重合的位置吗?若不能,请直接回答;若能,请直接指出,第几次移动,与哪一点重合.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com