
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)命题的题设为“两组对边分别相等的四边形”,结论是“是平行四边形”,即可得到结论;
(2)连接BD,利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC,∠ABD=∠CDB,进而可得AB∥CD,AD∥CB,根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形;
(3)把命题“两组对边分别相等的四边形是平行四边形”的题设和结论对换可得平行四边形两组对边分别相等.
试题解析:解:(1)已知:如图1,在四边形ABCD中,BC=AD,AB=CD.
求证:四边形ABCD是平行四边形.
(2)证明:连接BD.
在△ABD和△CDB中,∵AB=CD,AD=BC,BD=DB,∴△ABD≌△CDB(SSS),
∴∠ADB=∠DBC,∠ABD=∠CDB,∴AB∥CD,AD∥CB,∴四边形ABCD是平行四边形;
(3)用文字叙述所证命题的逆命题为:
平行四边形两组对边分别相等.


科目:初中数学 来源: 题型:
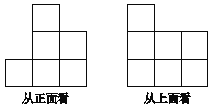
【题目】用大小相同的小立方块搭成一个几何体,使得从正面和上面看到的几何体的形状图如图19所示.
(1)这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
(2)画出这两种情况下从左面看到的几何体的形状图.(各画出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
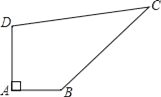
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,第一个图2条直线相交最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交最多有6个交点,…,像这样,则20条直线相交最多交点的个数是( )
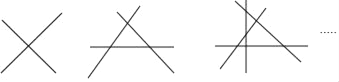
A. 171 B. 190 C. 210 D. 380
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( )
A.45°
B.30°
C.25°
D.15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() 是关于x的二次函数,求:
是关于x的二次函数,求:
(1)满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点;
(3)当k为何值时,函数有最小值?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘载重480 t的船,容积是1 050 m3,现有甲种货物450 m3,乙种货物350 t,而甲种货物每吨的体积为2.5 m3,乙种货物每立方米0.5 t.问:(1)甲、乙两种货物是否都能装上船?如果不能,请说明理由.
(2)为了最大限度地利用船的载质量和容积,两种货物应各装多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com