练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠BAC=90°，∠B=60°，△AB′C′可以由△ABC绕点A顺时针旋转90°得到（点B′与点B是对应点，点C′与点C是对应点），连接CC′，则∠CC′B′的度数是（　　）

    A.45°
    B.30°
    C.25°
    D.15°

    【答案】D
    【解析】由旋转的性质可知，AC=AC′，又∠CAC′=90°，可知△CAC′为等腰直角三角形，所以，∠CC′A=45°．∵∠CC′B′+∠ACC′=∠AB′C′=∠B=60°，
    ∴∠CC′B′=15°．故选D．
    【考点精析】掌握旋转的性质是解答本题的根本，需要知道①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD的长为6，宽为3，点O1为矩形的中心，⊙O2的半径为1，O1O2⊥AB于点P，O1O2=6．若⊙O2绕点P按顺时针方向旋转360°，在旋转过程中，⊙O2与矩形的边只有一个公共点的情况一共出现（　　）

    A.3次
    B.4次
    C.5次
    D.6次

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠BAC=90°，∠B=45°，BC=10 cm，过点A作AD∥BC，且点D在点A的右侧．点P从点A出发沿射线AD方向以每秒1cm的速度运动，同时点Q从点C出发沿射线CB方向以每秒2cm的速度运动，在线段QC上取点E，使得QE =2cm，连结PE，设点P的运动时间为t秒．

    （1）若PE⊥BC，则①PE= cm，CE= （用含t的式子表示）；

    ②求BQ的长；

    （2）请问是否存在t的值，使以A，B，E，P为顶点的四边形为平行四边形？若存在，求出t的值；若不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD，并写出了如下不完整的已知和求证．

    已知：如图1，在四边形ABCD中，BC=AD，AB=

    求证：四边形ABCD是 四边形．

    （1）在方框中填空，以补全已知和求证；

    （2）按嘉淇同学的思路写出证明过程；

    （3）用文字叙述所证命题的逆命题.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC绕着点C顺时针旋转50°后得到△A′B′C′．若∠A=40°．∠B′=110°，则∠BCA′的度数是（　　）

    A.110°
    B.80°
    C.40°
    D.30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′（此时，点B′落在对角线AC上，点A′落在CD的延长线上），A′B′交AD于点E，连接AA′、CE．
    求证：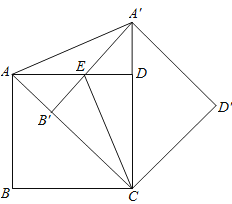

    （1）△ADA′≌△CDE；
    （2）直线CE是线段AA′的垂直平分线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，将腰CD以D为中心逆时针旋转90°至ED，连接AE、DE，△ADE的面积为3，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D，E分别是AC，AB上的两点，且 = = ，若△ADE的面积为1cm2 ， 则四边形EBCD的面积为（ ）cm2 ．

    A.2
    B.3
    C.4
    D.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△AOB为等腰三角形，顶点A的坐标（2， ），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，请你求出点O′的坐标．

    查看答案和解析>>

    同步练习册答案