Question

【题目】如图，△AOB为等腰三角形，顶点A的坐标（2， ），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，请你求出点O′的坐标．

Answer 1

【答案】

【解析】试题分析：过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，根据点A的坐标求出OC、AC，再利用勾股定理列式计算求出OA，根据等腰三角形三线合一的性质求出OB，根据旋转的性质可得BO′=OB，∠A′BO′=∠ABO，然后解直角三角形求出O′D、BD，再求出OD，然后写出点O′的坐标即可．

解：如图，过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D.

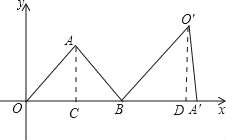
∵A（2，），

∴OC=2，AC=，

由勾股定理得，OA==3，

∵△AOB为等腰三角形，OB是底边，

∴OB=2OC=2×2=4，

由cos∠ABC==

∴=，

∴BD=

∴O′D==，

∴OD=OB+BD=4+=，

∴点O′的坐标为（，），