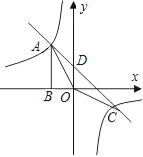
【题目】如图，Rt△ABO的顶点A是双曲线y＝
与直线y＝－x－(k＋1)在第二象限的交点．AB⊥x轴于B，且S△ABO＝
．
(1)求这两个函数的解析式；
(2)求直线与双曲线的两个交点A．C的坐标和△AOC的面积．
【答案】（1）y=﹣
，y=﹣x+2
（2）A为（﹣1，3），C为（3，﹣1），面积是4
【解析】试题分析：（1）欲求这两个函数的解析式，关键求k值．根据反比例函数性质，k绝对值为
且为负数，由此即可求出k；
（2）交点A、C的坐标是方程组
的解，解之即得；
（3）从图形上可看出△AOC的面积为两小三角形面积之和，根据三角形的面积公式即可求出．
解：（1）设A点坐标为（x，y），且x＜0，y＞0，
则S△ABO=
|BO||BA|=（﹣x）y=
，
∴xy=﹣3，
又∵y=
，
即xy=k，
∴k=﹣3．
∴所求的两个函数的解析式分别为y=﹣，y=﹣x+2；
（2）由y=﹣x+2，
令x=0，得y=2．
∴直线y=﹣x+2与y轴的交点D的坐标为（0，2），
A、C两点坐标满足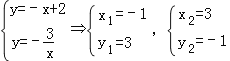
∴交点A为（﹣1，3），C为（3，﹣1），
∴S△AOC=S△ODA+S△ODC=
OD（|x1|+|x2|）=×2×（3+1）=4．
科目：初中数学 来源： 题型：
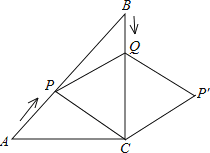
【题目】如图，在Rt△ABC中，∠C=90°，AC=BC=6cm，点P从点A出发，沿AB方向以每秒
cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿BC翻折，点P的对应点为点P′．设点Q运动的时间为t秒，若四边形QPCP′为菱形，则t的值为（ ）
A． B．2 C．2 D．3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在下列条件中，△ABC不是直角三角形的是 （ ）
A. b2=a2-c2 B. ∠A：∠B：∠C=3：4：5
C. ∠C=∠A-∠B D. a2：b2：c2=1：3：2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一副三角尺如图①摆放（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）点D为AB的中点，DE交AC于点P，DF经过点C．
（1）求∠ADE的度数；
（2）如图②，将△DEF绕点D顺时针方向旋转角α（0°<α<60°），此时的等腰直角三角尺记为△DE′F′，DE′交AC于点M，DF′交BC于点N，试判断
的值是否随着α的变化而变化？如果不变，请求出的值；反之，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】操作与探索：
在图①～③中，△ABC的面积为a.
(1)如图①，延长△ABC的边BC到点D，使CD＝BC，连接DA，若△ACD的面积为S1，则S1＝________(用含a的式子表示)；
(2)如图②，延长△ABC的边BC到点D，延长边CA到点E，使CD＝BC，AE＝CA，连接DE，若△DEC的面积为S2，则S2＝________(用含a的式子表示)，请说明理由；
(3)如图③，在图②的基础上延长AB到点F，使BF＝AB，连接FD，FE，得到△DEF，若阴影部分的面积为S3，则S3＝________(用含a的式子表示)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填写下面证明过程中的推理依据：
已知AD⊥BC，FG⊥BC，垂足分别为D、G，且∠1=∠2，求证∠BDE=∠C．
证明：∵AD⊥BC，FG⊥BC （已知），
∴∠ADC=∠FGC=90°____________．
∴AD∥FG______________________．
∴∠1=∠3___________________
又∵∠1=∠2，（已知），
∴∠3=∠2____________．
∴ED∥AC_____________．
∴∠BDE=∠C______________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工艺品厂生产一种汽车装饰品，每件生产成本为20元，销售价格在30元至80元之间（含30元和80元），销售过程中的管理、仓储、运输等各种费用（不含生产成本）总计50万元，其销售量y（万个）与销售价格（元/个）的函数关系如图所示．
（1）当30≤x≤60时，求y与x的函数关系式；
（2）求出该厂生产销售这种产品的纯利润w（万元）与销售价格x（元/个）的函数关系式；
（3）销售价格应定为多少元时，获得利润最大，最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为(0，3)，点A在x轴的负半轴上，点D、M分别在边AB、OA上，且AD＝2DB，AM＝2MO，一次函数y＝kx＋b的图象过点D和M，反比例函数y＝
的图象经过点D，与BC的交点为N.
(1)求反比例函数和一次函数的解析式；
(2)若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线l1∥l2，且l3和l1，l2分别交于A，B两点，点P在AB上.
(1)试找出∠1，∠2，∠3之间的关系并说出理由；
(2)如果点P在A，B两点之间运动，问∠1，∠2，∠3之间的关系是否发生变化？
(3)如果点P在A，B两点外侧运动，试探究∠1，∠2，∠3之间的关系(点P和A，B不重合).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com