
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?

【答案】(1)y=﹣0.1x+8(30≤x≤60)(2)w=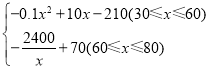 (3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
(3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
【解析】
试题分析:(1)由图象知,当30≤x≤60时,图象过(60,2)和(30,5),运用待定系数法求解析式即可;
(2)根据销售产品的纯利润=销售量×单个利润,分30≤x≤60和60<x≤80列函数表达式;
(3)当30≤x≤60时,运用二次函数性质解决,当60<x≤80时,运用反比例函数性质解答.
试题解析:(1)当x=60时,y=![]() =2,
=2,
∴当30≤x≤60时,图象过(60,2)和(30,5),
设y=kx+b,则
![]() ,
,
解得:![]() ,
,
∴y=﹣0.1x+8(30≤x≤60);
(2)根据题意,当30≤x≤60时,W=(x﹣20)y﹣50=(x﹣20)(﹣0.1x+8)﹣50=﹣0.1x2+10x﹣210,
当60<x≤80时,W=(x﹣20)y﹣50=(x﹣20)·![]() ﹣50=﹣
﹣50=﹣![]() +70,
+70,
综上所述:W=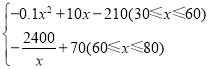 ;
;
(3)当30≤x≤60时,W=﹣0.1x2+10x﹣210=﹣0.1(x﹣50)2+40,
当x=50时,W最大=40(万元);
当60<x≤80时,W=﹣![]() +70,
+70,
∵﹣2400<0,W随x的增大而增大,
∴当x=80时,W最大=﹣![]() +70=40(万元),
+70=40(万元),
答:当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元.


科目:初中数学 来源: 题型:
【题目】下表所示为装运、销售甲、乙、丙三种蔬菜的重量及利润。某公司计划用20辆汽车装运甲、乙、丙三种蔬菜共36吨到某地销售.规定每辆汽车满载,每车只装一种蔬菜,每种蔬菜不少于一车。应如何安排,可使公司获得利润18300元?
甲 | 乙 | 丙 | |
每辆汽车装运的吨数 | 2 | 1 | 1.5 |
每吨蔬菜可获利润(百元) | 5 | 7 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC为等边三角形,P为BC上一点,Q为AC上一点,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则对下面四个结论判断正确的是( )

①点P在∠BAC的平分线上, ②AS=AR, ③QP∥AR, ④△BRP≌△QSP.
A. 全部正确; B. 仅①和②正确; C. 仅②③正确; D. 仅①和③正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y=![]() 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A.C的坐标和△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2+bx+c=0变形为:
x2+![]() x=﹣
x=﹣![]() ,…第一步
,…第一步
x2+![]() x+(
x+(![]() )2=﹣
)2=﹣![]() +(
+(![]() )2,…第二步
)2,…第二步
(x+![]() )2=
)2=![]() ,…第三步
,…第三步
x+![]() =
=![]() (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步
x=![]() ,…第五步
,…第五步
嘉淇的解法从第 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E分别在边AB、AC上,DE∥BC.

(1)试问△ADE是否是等腰三角形,并说明理由.
(2)若M为DE上的点,且BM平分![]() ,CM平分
,CM平分![]() ,若
,若![]() 的周长为20,BC=8.求
的周长为20,BC=8.求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数![]() 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.
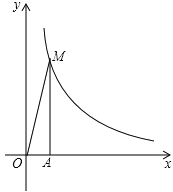
(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数![]() 的图象上,求t的值.
的图象上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com