
【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)点D为AB的中点,DE交AC于点P,DF经过点C.

(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断![]() 的值是否随着α的变化而变化?如果不变,请求出
的值是否随着α的变化而变化?如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
【答案】(1)30°;(2)![]() 的值不会随着α的变化而变化。
的值不会随着α的变化而变化。![]() .
.
【解析】试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得CD=AD=BD=![]() AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC-∠EDF计算即可得解;
AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC-∠EDF计算即可得解;
(2)根据同角的余角相等求出∠PDM=∠CDN,再根据然后求出△BCD是等边三角形,根据等边三角形的性质求出∠BCD=60°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CPD=60°,从而得到∠CPD=∠BCD,再根据两组角对应相等,两三角形相似判断出△DPM和△DCN相似,再根据相似三角形对应边成比例可得![]() 为定值.
为定值.
试题解析:(1)由题意知: CD是Rt△ABC中斜边AB上的中线,
∴AD=BD=CD,
∵在△BCD中,BD=CD且∠B=60°,
∴△BCD是等边三角形,
∴∠BCD=∠BDC=60°,
∴∠ADE=180°-∠BDC-∠EDF=180°-60°-90°=30°
(2)![]() 的值不会随着α的变化而变化。
的值不会随着α的变化而变化。
理由如下:∵△APD的外角∠MPD=∠A+∠ADE=30°+30°=60°,
∴∠MPD=∠BCD=60°.
∵在△MPD和△NCD中,∠MPD=∠NCD=60°,∠PDM=∠CDN=α,
∴△MPD∽△NCD,![]() ,
,
又∵由(1)知AD=CD,
∴∠ACD=∠A=30°,即∠PCD=30°.
在Rt△PCD中,∠PCD=30°,
∴![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
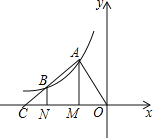
【题目】如图,点A、B在反比例函数y=![]() 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
A.2 B.4 C.﹣2 D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.

(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是:______;
(3)画出△ABC中AB边上的中线CE;
(4)平移过程中,线段AC扫过的面积是_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的括号内
-π, ![]() ,3.1,
,3.1, ![]() ,0.8080080008...(相邻两个8之间0的个数逐次增加1),
,0.8080080008...(相邻两个8之间0的个数逐次增加1), ![]() -
-![]() ,
, ![]() ,
, ![]() ,
, ![]()
整数集合{ }
负分数集合{ …}
正数集合{ …}
负数集合{ …}
有理数集合{ …}
无理数集合{ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC为等边三角形,P为BC上一点,Q为AC上一点,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则对下面四个结论判断正确的是( )

①点P在∠BAC的平分线上, ②AS=AR, ③QP∥AR, ④△BRP≌△QSP.
A. 全部正确; B. 仅①和②正确; C. 仅②③正确; D. 仅①和③正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M.
(1)如果AB=AC,求证:△DEF是等边三角形;
(2)如果AB≠AC,试猜想△DEF是不是等边三角形?如果△DEF是等边三角形,请加以证明;如果△DEF不是等边三角形,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y=![]() 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A.C的坐标和△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E分别在边AB、AC上,DE∥BC.

(1)试问△ADE是否是等腰三角形,并说明理由.
(2)若M为DE上的点,且BM平分![]() ,CM平分
,CM平分![]() ,若
,若![]() 的周长为20,BC=8.求
的周长为20,BC=8.求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com