
【题目】如图,在三角形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径作
为直径作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,直线
,直线![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
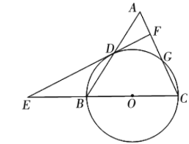
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD和CD,根据圆周角定理求出∠BDC=90°,根据等腰三角形的性质求出AD=BD,根据三角形的中位线求出OD∥AC,求出OD⊥EF,根据切线的判定得出即可;
(2)根据余角的性质得到∠ADF=∠ODC,等量代换得到∠ADF=∠OCD,根据勾股定理得到CD=12,根据三角函数的定义即可得到结论.
(1)证明:如图,连接OD,CD,
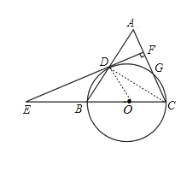
∵BC为⊙O的直径,
∴∠BDC=90°(直径所对的圆周角是90°),
即CD⊥AB,
∵AC=BC,AB=10,
∴AD=BD=5,
∵O为BC中点,
∴OD∥AC,
∵DF⊥AC,
∴∠DFC=90°,
∴∠FDO=180°-90°=90°(两直线平行,同旁内角互补),
∴OD⊥EF,
又∵OD过圆心O点,
∴直线DF是⊙O的切线;
(2)∵∠ADC=∠BDC=90°,∠ODF=90°,
∴∠ADF=∠ODC,
又∵OD=OC,
∴∠ODC=∠OCD,
∴∠ADF=∠OCD(等量替换),
∵BD=5,BC=13,
∴CD=![]() = 12(勾股定理),
= 12(勾股定理),
![]() ;
;


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
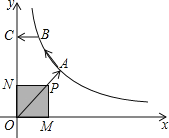
【题目】如图,已知点A是直线y=x与反比例函数y=(k>0,x>0)的交点,B是y=图象上的另一点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
A.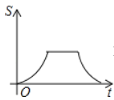 B.
B.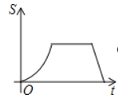 C.
C.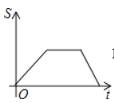 D.
D.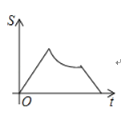
查看答案和解析>>
科目:初中数学 来源: 题型:
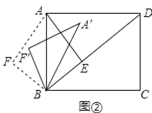
【题目】已知:如图①,在矩形ABCD中,AB=5,![]() ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
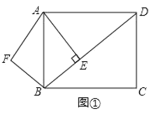
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,求出相应的m的值;
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的![]() 为
为![]() ,在旋转过程中,设
,在旋转过程中,设![]() 所在的直线与直线AD交于点P,与直线BD交于点Q,若△DPQ为等腰三角形,请直接写出此时DQ的长.
所在的直线与直线AD交于点P,与直线BD交于点Q,若△DPQ为等腰三角形,请直接写出此时DQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB是半圆O的直径,正方形OPNM的对角线ON与AB垂直且相等,Q是OP的中点.一只机器甲虫从点A出发匀速爬行,它先沿直径爬到点B,再沿半圆爬回到点A,一台微型记录仪记录了甲虫的爬行过程.设甲虫爬行的时间为t,甲虫与微型记录仪之间的距离为y,表示y与t的函数关系的图象如图2所示,那么微型记录仪可能位于图1中的( )
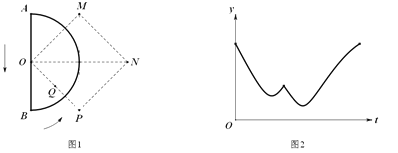
A.点MB.点NC.点PD.点Q
查看答案和解析>>
科目:初中数学 来源: 题型:
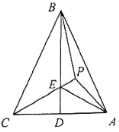
【题目】如图,P为等腰△ABC内一点,AB=BC,∠BPC=108°,D为AC中点,BD与PC相交于点E,已知P为△ABE的内心.
(1)求证:∠PEB=60°;
(2)求∠PAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是______________.(填序号)
;④0<CE≤6.4.其中正确的结论是______________.(填序号) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com