
【题目】如图,P为等腰△ABC内一点,AB=BC,∠BPC=108°,D为AC中点,BD与PC相交于点E,已知P为△ABE的内心.
(1)求证:∠PEB=60°;
(2)求∠PAC的度数.
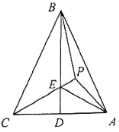
【答案】(1)见解析 (2)48°
【解析】
(1)先由P为△ABE的内心,∠BPC=108°易知∠BAE=36°,再由△ABC为等腰三角形,D为AC中点,∠BPC=108°得到∠CBE=∠ABE=2∠PBE,且∠CBP=∠BCP=∠BAE=36°,即可得到∠CBE=24°,再利用∠PEB=∠BCE+∠CBE得证.
(2)易知∠AED=∠CED=∠BEP=60°,从而得到∠EAD=30,利用∠PAC=∠EAD+∠PAE即可得解.
(1)∵P为△ABE内心,
∴PB、PE、PA分别是∠ABE、∠AEB、∠BAE角平分线;
即:∠PBE+∠PEB+∠PAE=90°,
又∵∠BPC=108°,
∴∠PBE+∠PEB=72°,
∴∠PAE=18°,∠BAE=36°;
∵AB=BC且D是AC中点,
∴∠ABE=∠CBE;BD⊥AC,
又∵BE=BE,AB=CB;
∴△ABE≌△CBE;即∠BCE=∠BAE=36°;
又∵∠BPC=108°,
∴∠CBP=36°,
∵又∠CBE=∠ABE=2∠PBE;
设∠PBE=∠ABP=x,则∠CBE=2x, 由∠CBP=∠CBE+∠PBE=36°,有2x+x=36°,
∴x=12°,
所以∠CBE=2x=24°,所以∠PEB=∠BCE+∠CBE=36°+2×14°=60°;
(2)由(1)知△ABE≌△CBE;
∴∠BEC=∠BEA,
∴∠CED=∠AED=∠PEB=60°;
∴∠EAD=30°,
∴∠PAC=∠EAD+∠PAE =30°+18°=48°。


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
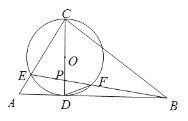
【题目】如图,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交AC于E,连接BE交CD于P,交⊙O于F,连接DF,∠ABC=∠EFD.
(1)求证:AB与⊙O相切;
(2)若AD=4,BD=6,则⊙O的半径= ;
(3)若PC=2PF,BF=a,求CP(用a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
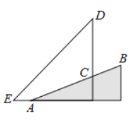
【题目】在屋楼崮西侧一个坡度(或坡比)![]() 的山坡
的山坡![]() 上发现有一棵古树
上发现有一棵古树![]() .测得古树底端
.测得古树底端![]() 到山脚点
到山脚点![]() 的距离
的距离![]() 米,在距山脚点
米,在距山脚点![]() 水平距离
水平距离![]() 米的点
米的点![]() 处,测得古树顶端
处,测得古树顶端![]() 的仰角
的仰角![]() (古树
(古树![]() 与山坡
与山坡![]() 的剖面、点
的剖面、点![]() 在同一平面上,古树
在同一平面上,古树![]() 与直线
与直线![]() 垂直),则古树
垂直),则古树![]() 的高度约为
的高度约为![]() ( )
( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A坐标为(-8,0),点B坐标为(0,6),⊙O的半径为4(O为坐标原点),点C是⊙O上一动点,过点B作直线AC的垂线BP,P为垂足.点C在⊙O上运动一周,则点P运动的路径长等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
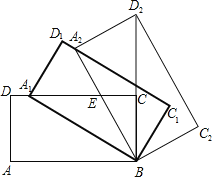
【题目】如图,矩形ABCD中,AB=m,BC=n,将此矩形绕点B顺时针方向旋转θ(0°<θ<90°)得到矩形A1BC1D1,点A1在边CD上.
(1)若m=2,n=1,求在旋转过程中,点D到点D1所经过路径的长度;
(2)将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2,点D2在BC的延长线上,设边A2B与CD交于点E,若![]() =
=![]() ﹣1,求
﹣1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
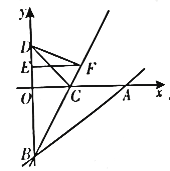
【题目】如图,在平面直角坐标系xOy中,直线![]() 交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将
交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将![]() 沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
(1)求直线AB的表达式.
(2)已知点E(0,3),点P是直线BC上的一个动点(点P不与点B重合),连接PD,PE,当![]() PDE的周长取得最小值时,求点P的坐标。
PDE的周长取得最小值时,求点P的坐标。
(3)在坐标轴上是否存在一点H,使得![]() HAB和
HAB和![]() ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
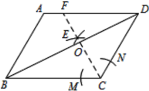
【题目】如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°. 按以下步骤作图:①以C为圆心,以适当长为半径做弧,交CB、CD于M、N两点;②分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com