
【题目】如图,已知平行四边形![]() 中,
中,![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长,交
并延长,交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() ;
;
(2)连接![]() ,
,![]() ,当
,当![]() _______°时,四边形
_______°时,四边形![]() 是正方形?
是正方形?
【答案】(1)见解析;(2)45
【解析】
(1)根据平行线的性质可得∠D=∠OCE,∠DAO=∠E,再根据中点定义可得DO=CO,然后可利用AAS证明△AOD≌△EOC;
(2)当∠B=∠AEB=45°时,四边形ACED是正方形,首先证明四边形ACED是平行四边形,再证对角线互相垂直且相等可得四边形ACED是正方形.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
∵O是CD的中点,
∴OC=OD,
在△ADO和△ECO中,
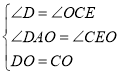 ,
,
∴△AOD≌△EOC(AAS);
(2)当∠B=∠AEB=45°时,四边形ACED是正方形.
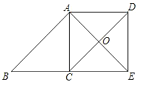
∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,
∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.
∴ACED是菱形.
∵AB=AE,AB=CD,
∴AE=CD.
∴菱形ACED是正方形.
故答案为:45.


科目:初中数学 来源: 题型:
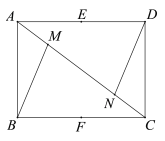
【题目】如图,在矩形ABCD中,AB=3,BC=4.M、N在对角线AC上,且AM=CN,E、F分别是AD、BC的中点.
(1)求证:△ABM≌△CDN;
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别在钱段AB、AC上,CD与BE交于O,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD

A. ∠B=∠CB. AD=AEC. BE=CDD. BD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(k-1)x2+2kx+2=0
(1)求证:无论k为何值,方程总有实数根.
(2)设x1,x2是该方程的两个根,记S=x1+x2-x1x2,S的值能为0吗?若能,求出此时k的值.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的![]() .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的![]() ,求道路的宽.
,求道路的宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.当AB与BC满足___________条件时,四边形AEOF正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(40,0)和(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动、动直线EF从x轴开始以每秒1个单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)求t=15时,△PEF的面积;
(2)直线EF、点P在运动过程中,是否存在这样的t,使得△PEF的面积等于160(平方单位)?若存在,请求出此时t的值;若不存在,请说明理由.
(3)当t为何值时,△EOP与△BOA相似.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com