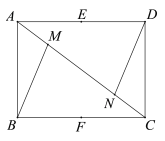
【题目】如图，在矩形ABCD中，AB=3，BC=4．M、N在对角线AC上，且AM=CN，E、F分别是AD、BC的中点．
（1）求证：△ABM≌△CDN；
（2）点G是对角线AC上的点，∠EGF=90°，求AG的长．
【答案】（1）见解析；（2）AG的长为1或4．
【解析】
（1）根据四边形的性质得到AB∥CD，求得∠MAB=∠NCD．根据全等三角形的判定定理得到结论；
（2）连接EF，交AC于点O．根据全等三角形的性质得到EO=FO，AO=CO，于是得到结论．
（1）证明∵四边形ABCD是矩形，∴AB∥CD，∴∠MAB = ∠NCD．
在△ABM和△CDN中，
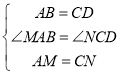
∴△ABM≌△CDN；
（2）解：如图，连接EF，交AC于点O．
在△AEO和△CFO中，
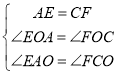
∴△AEO≌△CFO，∴EO=FO，AO=CO，∴O为EF、AC中点．
∵∠EGF=90°，
，∴AG=OA-OG =1或AG=OA+OG=4，
∴AG的长为1或4．
高效智能课时作业系列答案
捷径训练检测卷系列答案科目：初中数学 来源： 题型：
【题目】为加强中小学生安全和禁毒教育，某校组织了“防溺水、交通安全、禁毒”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），购买1个足球和1个篮球共需159元；足球单价是篮球单价的2倍少9元．
（1）求足球和篮球的单价各是多少元？
（2）根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，学校最多可以购买多少个足球？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点D是等边△ABC(即三条边都相等，三个角都相等的三角形)边BA上任意一点(点D与点B不重合)，连接DC．
(1)如图1，以DC为边在BC上方作等边△DCF，连接AF，猜想线段AF与BD的数量关系？请说明理由．
(2)如图2，若以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′，连接AF、BF′，探究AF、BF′与AB有何数量关系？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．
(1)、如图①，对△ABC作变换[50°，
]得△AB′C′，则S△AB′C′：S△ABC= ；直线BC与直线B′C′所夹的锐角为 度；
(2)、如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB'C'，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；
(3)、如图③，△ABC中，AB=AC，∠BAC=36°，BC=l，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ和n的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将长方形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC=62°，则∠DFE的度数为（ ）
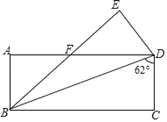
A. 62°B. 56°C. 31°D. 28°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将三角形ABC向右平移5个单位长度，再向上平移3个单位长度请回答下列问题：
（1）平移后的三个顶点坐标分别为：A1 ，B1 ，C1 ；
（2）画出平移后三角形A1B1C1；
（3）求三角形ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
