
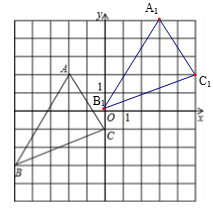
【题目】如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.

【答案】(1)A1(4,7),B1(1,2),C1(6,4);(2)略;(3)![]()
【解析】
(1)根据平移的规律变化结合平面直角坐标系写出各点的坐标即可;
(2)根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;
(3)利用△ABC所在的矩形的面积减去四周三个直角三角形的面积,列式计算即可得解.
(1) 观察图形可知点A(-2,2),点B(-5,-3),点C(0,-1),
所以将三角形ABC向右平移5个单位长度,再向上平移3个单位长度后所得对应点的坐标为:A1(3,5),B1(0,0),C1(5,2);
(2)△A1B1C1如图所示;
(3)△ABC的面积=5×5-![]() ×5×2-
×5×2-![]() ×2×3-
×2×3-![]() ×3×5
×3×5
=25-5-3-7.5
=25-15.5
=9.5.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
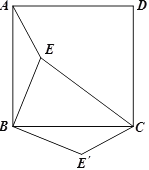
【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求EE′的长?并求出∠BE′C的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
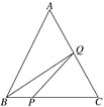
【题目】在△ABC中,已知AB=BC=CA=4 cm,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1 cm/s;点Q沿CA、AB向终点B运动,速度为2 cm/s,设它们运动的时间为x(s),当x=__________,△BPQ是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°.点D是AB中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.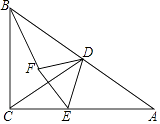
(1)△BCD的形状为;
(2)随着点E位置的变化,∠DBF的度数是否变化?并结合图说明你的理由;
(3)当点F落在边AC上时,若AC=6,请直接写出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级学生在5 名教师的带领下去动物园秋游,动物园的门票为每 人40 元,现有两种优惠方案,甲方案:带队教师免费,学生按8 折收费;乙 方案:师生都7.5 折收费.
(1)若有m 名学生,用含m 的式子表示两种优惠方案各需多少元?
(2)当m=70 时,采用哪种方案优惠?
(3)当m=100 时,采用哪种方案优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,在数轴上,|a|表示数a到原点的距离,这是绝对值的几 何意义,进一步地,数轴上两个点A、B,分别用a 和b 表示,那么A、B两点之间的距离为AB=|a﹣b|利用此结论,回答以下问题:
(1)数轴上表示3 和7 的两点之间的距离是 ,数轴上表示﹣3 和﹣7 的两 点之间的距离是 ,数轴上表示2 和﹣3 的两点之间的距离是 ;
(2)数轴上表示x和﹣5 的两点A、B之间的距离是 ,如果|AB|=3,那 么x的值为 ;
(3)当代数式|x﹣1|+|x﹣3|取最小值时,相应的x的取值范围是多少?最小值是多少?
(4)已知点A在数轴上对应的数是a,点B在数轴上对应的数是b,且|a+4|+(b﹣1)2=0,设点P在数轴上对应的数是x,当|PA|﹣|PB|=2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E. 
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题3tan30°﹣|﹣2|+ ![]() +(﹣1)2017;
+(﹣1)2017;
(1)计算:3tan30°﹣|﹣2|+ ![]() +(﹣1)2017;
+(﹣1)2017;
(2)解方程: ![]() =
= ![]() ﹣2.
﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:

![]()
![]()
![]()
⑴ 当黑砖n=1时,白砖有_______块,当黑砖n=2时,白砖有________块,
当黑砖n=3时,白砖有_______块.
⑵ 第n个图案中,白色地砖共 块.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com