
����Ŀ������֪�����������ϣ�|a|��ʾ��a��ԭ��ľ��룬���Ǿ���ֵ�ļ� �����壬��һ���أ�������������A��B���ֱ���a ��b ��ʾ����ôA��B����֮��ľ���ΪAB��|a��b|���ô˽��ۣ��ش��������⣺
(1)�����ϱ�ʾ3 ��7 ������֮��ľ����� �������ϱ�ʾ��3 �ͩ�7 ���� ��֮��ľ����� �������ϱ�ʾ2 �ͩ�3 ������֮��ľ����� ��
(2)�����ϱ�ʾx�ͩ�5 ������A��B֮��ľ����� �����|AB|��3���� ôx��ֵΪ ��
(3)������ʽ|x��1|+|x��3|ȡ��Сֵʱ����Ӧ��x��ȡֵ��Χ�Ƕ��٣���Сֵ�Ƕ��٣�
(4)��֪��A�������϶�Ӧ������a����B�������϶�Ӧ������b����|a+4|+(b��1)2��0�����P�������϶�Ӧ������x����|PA|��|PB|��2ʱ����x��ֵ��
���𰸡�(1)4��4��5��(2)![]() ��-8��-2��(3)x�ķ�Χ��
��-8��-2��(3)x�ķ�Χ��![]() ����Сֵ��4��(4)x��ֵΪ
����Сֵ��4��(4)x��ֵΪ![]() .
.
��������
��1����2��ֱ�Ӹ���������A��B����֮��ľ���|AB|=|a��b|��������ֵ���þ���ֵ���������������ľ��룮
��3������|x��a|��ʾ������x��a֮��ľ��룬���ԭʽ��ʾ��������һ�㵽1��3����ĺͣ���x��1��3֮��ʱ����Сֵ��
��4��Ӧ���ǵ�A��B��P����֮���λ�ù�ϵ�Ķ��ֿ��ܽ��⣮
��1�������ϱ�ʾ3��7������֮��ľ�����|7��3|=4�������ϱ�ʾ��3�ͩ�7������֮��ľ�����|��7������3��|=4�������ϱ�ʾ2�ͩ�3������֮��ľ�����|2������3��|=5��
��2�������ϱ�ʾx�ͩ�5������A��B֮��ľ�����|x������5��|=|x+5|�����|AB|=3����ôxΪ��8��2��
��3������ʽ|x��1|+|x+3|��ʾ�������ϵ�1�ͩ�3����ľ���ĺͣ���x�ک�3��1֮��ʱ������ʽȡ����Сֵ����Сֵ�ǩ�3��1֮��ľ���4��
�ʵ���3��x��1ʱ������ʽȡ����Сֵ����Сֵ��4��
��4���ٵ�P�ڵ�A���ʱ��|PA|��|PB|=����|PB|��|PA|��=��|AB|=��5��2��
�ڵ�P�ڵ�B�Ҳ�ʱ��|PA|��|PB|=|AB|=5��2����������������ĵ�P�����ڣ�
�۵�P��A��B֮��ʱ��|PA|=|x������4��|=x+4��|PB|=|x��1|=1��x��
��|PA|��|PB|=2����x+4����1��x��=2����x![]() ����x��ֵΪ
����x��ֵΪ![]() ��
��
�ʴ�Ϊ����1��4��4��5��
��2��|x+5|����8��2��
��3��x�ķ�Χ�ǩ�3��x��1����Сֵ��4��
��4��x��ֵΪ-![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90![]() ����BAC��ƽ���߽�BC��D������C��CG��AB��G����AD��E������D��DF��AB��F.���н��ۢ١�CED=
����BAC��ƽ���߽�BC��D������C��CG��AB��G����AD��E������D��DF��AB��F.���н��ۢ١�CED= ![]() ����
����![]() ���ۡ�ADF=
���ۡ�ADF= ![]() ;��CE=DF.��ȷ������ ��
;��CE=DF.��ȷ������ ��

A. �٢ڢ� B. �ڢۢ� C. �٢� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��ǽ��AOB��OA��OB����OA��OB���Ȳ��ޣ��У�Ҫ��20m����ǽ����ֱ��ǽ��AOBΧ�ɵ���Ϊ���εĴ��֣��ҵ������AOBC�����Ϊ96m2 �� 
��1�����������εij���
��2���й��Ϊ0.80��0.80��1.00��1.00����λ��m���ĵذ�ש���۷ֱ�Ϊ55Ԫ/���80Ԫ/�飬��ֻѡ����һ�ֵذ�ש��ǡ�����������ֵľ��ε��棨���Ʒ�϶��������һ�ֹ��ĵذ�ש���ý��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̲ĵھ�����̽���˷���ʽʱ��������ͼ������IJ�ͬ��ʾ������֤�˳˷���ʽ���ҹ���������ѧ����ˬ�����ڹ�Ԫ3���ͣ��Ͱ�һ�����ηֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ĸ�ȫ�ȵ�ֱ��������ƴ����һ�����������(��ͼ��)�����ͼ�γ�Ϊ��ˬ��ͼ����֤��һ���dz���Ҫ�Ľ��ۣ���ֱ������������ֱ�DZ�a��b��б��c�����ϵʽa2��b2��c2����Ϊ���ɶ�����
(1)�����Խ��С�������ĸ�ȫ�ȵ�ֱ��������ƴ������һ�����������(��ͼ��)��Ҳ����֤������ۣ��������С�������֤�Ĺ��̣�
(2)С���ְ����ĸ�ȫ�ȵ�ֱ��������ƴ����һ������(��ͼ��)����������̽�����ý��ۣ���a��3��b��4ʱ����ABCD���ܳ���
(3)��ͼ�ܣ���ÿ��С�����α߳�Ϊ1�ķ���ֽ�У���ABC�Ķ��㶼�ڷ���ֽ����ϣ�����ͼ�л�����ABC�ĸ�BD����������Ľ��ۣ����BD�ij���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC����ƽ��5����λ���ȣ�������ƽ��3����λ������ش��������⣺
��1��ƽ�ƺ��������������ֱ�Ϊ��A1�� ����B1�� ����C1�� ����
��2������ƽ�ƺ�������A1B1C1��
��3����������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c�IJ���ͼ����ͼ��ʾ�������x�ķ���ax2+bx+c=0���������ĺ�Ϊ �� 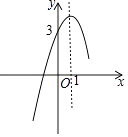
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������(1)��A=25������B=65����(2)3��A=2��B=��C��(3)��A=5��B��(4)2��A=3��B=4��C�У�������ȷ����ABC��ֱ�������ε�������( )
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC����A1B1C1���ڵ�E�����ĶԳƣ�

��1�������Գ�����E����д����E��A��C�����ꣻ
��2��P��a��b������ABC�ı�AC��һ�㣬��ABC��ƽ�ƺ��P�Ķ�Ӧ��ΪP2��a+6��b+2�����뻭������ƽ�ƺ����A2B2C2����д����A2��C2�����ꣻ
��3���ж���A2B2C2����A1B1C1��λ�ù�ϵ��ֱ��д���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��������![]() Ԫ�ij˳�IC����������˳��Ĵ�����
Ԫ�ij˳�IC����������˳��Ĵ�����![]() ��ʾ�����¼��ÿ�γ˳�������
��ʾ�����¼��ÿ�γ˳�������![]() ��Ԫ�����±���
��Ԫ�����±���
����m | ���n��Ԫ�� |
1 | 50��0.8 |
2 | 50��1.6 |
3 | 50��2.4 |
4 | 50��3.2 |
���� | ���� |
��1����д���˳��Ĵ���![]() ��ʾ���
��ʾ���![]() ��Ԫ���Ĺ�ϵʽ��
��Ԫ���Ĺ�ϵʽ��
��2��������������ϵʽ����С�ų���13�γ���ʣ�¶���Ԫ��
��3����С������ܳ˼��γ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com