
【题目】在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2 . 
(1)求这地面矩形的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
科目:初中数学 来源: 题型:
【题目】某班将举行知识竞赛活动,班长安排小明购买奖品.小明去文化用品店买了两种大小不同的笔记本一共a本,其中大笔记本单价8元,小笔记本单价5元.若设买单价5元小笔记本买了x本.
(1)填写下表:
单价(元/本) | 数量(本) | 金额(元) | |
小笔记本 | 5 | x | 5x |
大笔记本 | 8 |
(2)列式表示:小明买大小笔记本共花 元.
(3)若小明从班长那里拿了300元,买了40本大小不同的两种笔记本(a=40),还找回55元给班长,那么小明买了大小笔记本各多少本?
(4)若这个班下次活动中,让小明刚好花400元购买这两种大小笔记本,并且购买的小笔记本数量x要小于60本,但还要超过30本(30<x<60),请列举小明有可能购买的方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一中学有学生3000名,2016年母亲节,晓彤为了调查本校大约有多少学生知道自己母亲的生日,随机调查了200名学生,有20名同学不知道自己母亲生日,关于这个数据收集和处理的问题,下列说法错误的是( )
A.个体是该校每一位学生
B.本校约有300名学生不知道自己母亲的生日
C.调查的方式是抽样调查
D.样本是随机调查的200名学生是否知道自己母亲的生日
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由6个正方形拼成的一个长方形,如果最小的正方形的边长为1
(Ⅰ)能否求出拼成的长方形的面积?____(填“能”或“不能”);
(Ⅱ)若能,请你写出拼成的长方形的面积;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,已知AB=BC=CA=4 cm,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1 cm/s;点Q沿CA、AB向终点B运动,速度为2 cm/s,设它们运动的时间为x(s),当x=__________,△BPQ是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网站策划了A、B两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 30 | 25 | 0.05 |
B | m | n | P |
设每月上网学习时间为x(h)小时,方案A,B的收费金额分别为yA (元)、yB(元).
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)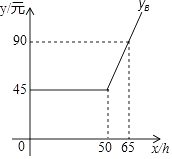
(1)m=;n=p= .
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°.点D是AB中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.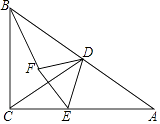
(1)△BCD的形状为;
(2)随着点E位置的变化,∠DBF的度数是否变化?并结合图说明你的理由;
(3)当点F落在边AC上时,若AC=6,请直接写出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,在数轴上,|a|表示数a到原点的距离,这是绝对值的几 何意义,进一步地,数轴上两个点A、B,分别用a 和b 表示,那么A、B两点之间的距离为AB=|a﹣b|利用此结论,回答以下问题:
(1)数轴上表示3 和7 的两点之间的距离是 ,数轴上表示﹣3 和﹣7 的两 点之间的距离是 ,数轴上表示2 和﹣3 的两点之间的距离是 ;
(2)数轴上表示x和﹣5 的两点A、B之间的距离是 ,如果|AB|=3,那 么x的值为 ;
(3)当代数式|x﹣1|+|x﹣3|取最小值时,相应的x的取值范围是多少?最小值是多少?
(4)已知点A在数轴上对应的数是a,点B在数轴上对应的数是b,且|a+4|+(b﹣1)2=0,设点P在数轴上对应的数是x,当|PA|﹣|PB|=2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com