
【题目】下列条件:(1)∠A=25°,∠B=65°;(2)3∠A=2∠B=∠C;(3)∠A=5∠B;(4)2∠A=3∠B=4∠C中,其中能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A
【解析】
根据三角形的内角和定理求出各小题中最大的角的度数即可进行判断.
(1)∵∠A=25°,∠B=65°,
∴∠A+∠B=25°+65°=90°,
又∵∠A+∠B+∠C=180°,
∴∠C=180°-(∠A+∠B)=180°-90°=90°,
∴△ABC是直角三角形;
(2)∵3∠A=2∠B=∠C,
∴∠A=![]() ∠C,∠B=
∠C,∠B=![]() ∠C,
∠C,
∵∠A+∠B+∠C=180°
∴![]() ∠C+
∠C+![]() ∠C+∠C=
∠C+∠C=![]() ∠C=180°
∠C=180°
∴∠C≠90°
∴△ABC不是直角三角形;
(3)∵∠A=5∠B
∴无法计算内角的度数,
因此无法判定△ABC的形状;
(4)∵2∠A=3∠B=4∠C,
∴∠A=2∠C,∠B=![]() ∠C,
∠C,
又∵∠A+∠B+∠C=180°,
∴2∠C+![]() ∠C+∠C=
∠C+∠C=![]() ∠C=180°,
∠C=180°,
∴∠C=![]()
∴△ABC不是直角三角形.
故选A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一中学有学生3000名,2016年母亲节,晓彤为了调查本校大约有多少学生知道自己母亲的生日,随机调查了200名学生,有20名同学不知道自己母亲生日,关于这个数据收集和处理的问题,下列说法错误的是( )
A.个体是该校每一位学生
B.本校约有300名学生不知道自己母亲的生日
C.调查的方式是抽样调查
D.样本是随机调查的200名学生是否知道自己母亲的生日
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°.点D是AB中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.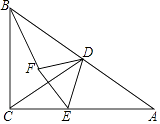
(1)△BCD的形状为;
(2)随着点E位置的变化,∠DBF的度数是否变化?并结合图说明你的理由;
(3)当点F落在边AC上时,若AC=6,请直接写出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,在数轴上,|a|表示数a到原点的距离,这是绝对值的几 何意义,进一步地,数轴上两个点A、B,分别用a 和b 表示,那么A、B两点之间的距离为AB=|a﹣b|利用此结论,回答以下问题:
(1)数轴上表示3 和7 的两点之间的距离是 ,数轴上表示﹣3 和﹣7 的两 点之间的距离是 ,数轴上表示2 和﹣3 的两点之间的距离是 ;
(2)数轴上表示x和﹣5 的两点A、B之间的距离是 ,如果|AB|=3,那 么x的值为 ;
(3)当代数式|x﹣1|+|x﹣3|取最小值时,相应的x的取值范围是多少?最小值是多少?
(4)已知点A在数轴上对应的数是a,点B在数轴上对应的数是b,且|a+4|+(b﹣1)2=0,设点P在数轴上对应的数是x,当|PA|﹣|PB|=2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E. 
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市上网有两种收费方案,用户可任选其一,A为计时制--1元![]() 时;B为包月制--80元
时;B为包月制--80元![]() 月,此外每种上网方式都附加通讯费
月,此外每种上网方式都附加通讯费![]() 元
元![]() 时.
时.
![]() 某用户每月上网40小时,选哪种方式比较合适?
某用户每月上网40小时,选哪种方式比较合适?
![]() 某用户每月有100元钱用于上网,选哪种方式比较合算?
某用户每月有100元钱用于上网,选哪种方式比较合算?
![]() 请你设计一个方案,使用户能合理地选择上网方式.
请你设计一个方案,使用户能合理地选择上网方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题3tan30°﹣|﹣2|+ ![]() +(﹣1)2017;
+(﹣1)2017;
(1)计算:3tan30°﹣|﹣2|+ ![]() +(﹣1)2017;
+(﹣1)2017;
(2)解方程: ![]() =
= ![]() ﹣2.
﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图放置,则下列结论中,正确的有( )①∠1=∠3;②如果∠2=30°则有AC∥DE;③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C

A.①②③B.①②④C.③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com