
【题目】如图,在Rt△ABC中,∠ACB=90![]() ,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED=
,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED= ![]() ;②
;②![]() ;③∠ADF=
;③∠ADF= ![]() ;④CE=DF.正确的是( )
;④CE=DF.正确的是( )

A. ①②④ B. ②③④ C. ①③ D. ①②③④
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)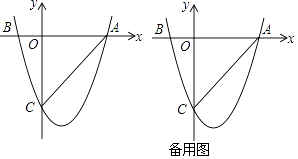
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行知识竞赛活动,班长安排小明购买奖品.小明去文化用品店买了两种大小不同的笔记本一共a本,其中大笔记本单价8元,小笔记本单价5元.若设买单价5元小笔记本买了x本.
(1)填写下表:
单价(元/本) | 数量(本) | 金额(元) | |
小笔记本 | 5 | x | 5x |
大笔记本 | 8 |
(2)列式表示:小明买大小笔记本共花 元.
(3)若小明从班长那里拿了300元,买了40本大小不同的两种笔记本(a=40),还找回55元给班长,那么小明买了大小笔记本各多少本?
(4)若这个班下次活动中,让小明刚好花400元购买这两种大小笔记本,并且购买的小笔记本数量x要小于60本,但还要超过30本(30<x<60),请列举小明有可能购买的方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导节能低碳的生活,某公司对集体宿舍用电收费作如下规定:一间宿舍一个月用电量不超过a千瓦时,则一个月的电费为20元;若超过a千瓦时,则除了交20元外,超过部分每千瓦时要交 ![]() 元.某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元.
元.某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元.
(1)求a的值;
(2)若该宿舍5月份交电费45元,那么该宿舍当月用电量为多少千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求EE′的长?并求出∠BE′C的度数?
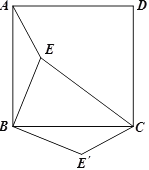
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一中学有学生3000名,2016年母亲节,晓彤为了调查本校大约有多少学生知道自己母亲的生日,随机调查了200名学生,有20名同学不知道自己母亲生日,关于这个数据收集和处理的问题,下列说法错误的是( )
A.个体是该校每一位学生
B.本校约有300名学生不知道自己母亲的生日
C.调查的方式是抽样调查
D.样本是随机调查的200名学生是否知道自己母亲的生日
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由6个正方形拼成的一个长方形,如果最小的正方形的边长为1
(Ⅰ)能否求出拼成的长方形的面积?____(填“能”或“不能”);
(Ⅱ)若能,请你写出拼成的长方形的面积;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,在数轴上,|a|表示数a到原点的距离,这是绝对值的几 何意义,进一步地,数轴上两个点A、B,分别用a 和b 表示,那么A、B两点之间的距离为AB=|a﹣b|利用此结论,回答以下问题:
(1)数轴上表示3 和7 的两点之间的距离是 ,数轴上表示﹣3 和﹣7 的两 点之间的距离是 ,数轴上表示2 和﹣3 的两点之间的距离是 ;
(2)数轴上表示x和﹣5 的两点A、B之间的距离是 ,如果|AB|=3,那 么x的值为 ;
(3)当代数式|x﹣1|+|x﹣3|取最小值时,相应的x的取值范围是多少?最小值是多少?
(4)已知点A在数轴上对应的数是a,点B在数轴上对应的数是b,且|a+4|+(b﹣1)2=0,设点P在数轴上对应的数是x,当|PA|﹣|PB|=2时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com