
����Ŀ������ABC�Ƶ�A����ʱ�뷽����ת���ȣ���ʹ���߳���Ϊԭ����n��������AB��C��������ͼ�������ǽ����ֱ任��Ϊ[����n]��

(1)����ͼ��������ABC���任[50����![]() ]����AB��C������S��AB��C����S��ABC= ��ֱ��BC��ֱ��B��C�����е����Ϊ �ȣ�
]����AB��C������S��AB��C����S��ABC= ��ֱ��BC��ֱ��B��C�����е����Ϊ �ȣ�
(2)����ͼ������ABC�У���BAC=30������ACB=90��������ABC ���任[����n]����AB'C'��ʹ��B��C��C����ͬһֱ���ϣ����ı���ABB'C'Ϊ���Σ�������n��ֵ��
(3)����ͼ������ABC�У�AB=AC����BAC=36����BC=l������ABC���任[����n]����AB��C����ʹ��B��C��B����ͬһֱ���ϣ����ı���ABB'C'Ϊƽ���ı��Σ�������n��ֵ��
���𰸡�(1)��5��50����(2)��60����2��(3)��72����![]() .
.
��������
���������(1)���������������Ƶ������Լ���תͼ�ε����ʵó��𰸣�(2)�����ȸ�����=��CAC'=��BAC'����BAC����Ƕȣ�Ȼ�����Rt��ABC�����ʵó�n��ֵ��(3)������ABB'C'��ƽ���ı����Լ���BAC=36���ó���=72����������C'AB'=��BAC=36������B=��B�ó���ABC�ס�B'BA���Ӷ����AB�ij���.
���������(1)��5�� 50��
(2)����=��CAC'=��BAC'����BAC=90�㩁30��=60��
�� Rt��ABC ����ABB'=90������BAB'=60����AB'B=30���� ��n=2
(3)�����ı���ABB'C'��ƽ���ı��Σ���AC'��BB'�����ߡ�BAC=36�������=��CAC'=��ACB=72����
���C'AB'=��BAC=36��������B=��B�����ABC�ס�B'BA��
��AB��BB'=CB��AB�� ��AB2=CB![]() BB'=CB��BC+CB'����
BB'=CB��BC+CB'����
�� CB'=AC=AB=B'C'�� BC=1�� ��AB2=1��1+AB���� ��AB=![]() ��
��
��AB��0�� ��n=![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC=90�㣬AD��BC����ABC��ƽ����BE��AD�ڵ�F��AGƽ�֡�DAC.�������н��ۣ��١�BAD=��C�� �ڡ�AEF=��AFE�� �ۡ�EBC=��C����AG��EF����ȷ�����У� ��
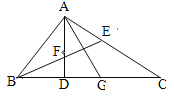
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����P������������һ�㣬����APB=��ABC��

��1����ͼ1������BAC=60������Pǡ������ABC��ƽ�����ϣ�PA=2����PB�ij���
��2����ͼ2������BAC=60����̽��PA��PB��PC��������ϵ����֤����
��3����ͼ3������BAC=120������ֱ��д��PA��PB��PC��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���P��1����1������ԭ��ĶԳƵ������Ϊ�� ��
A.��1��1��
B.��1����1��
C.����1��1��
D.����1����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ����֪����y= (x��0)ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b��(b>0) ������M��y���������ϵ�B�Ϸ��ĵ㣮����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q������AQ��ȡAQ���е�C��
(1)��ͼ2������BP������PAB�������
(2)����Q���߶�BD��ʱ, ���ı���BQNC�����Σ����Ϊ2�����ʱP������꣮
(3)��(2)�������£���ƽ��ֱ������ϵ���Ƿ���ڵ�S��ʹ���Ե�D��Q��N��SΪ������ı���Ϊƽ���ı�
�Σ�������ڣ���ֱ��д�����еĵ�S�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ������ ��
A. a2��a3��a6 B. ����2ab��2��4a2b2 C. ��a2��3��a5 D. a6��a3��a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е����У��ʺ��ղ���ǣ� ����
A. ��ѧ����ϲ���ĵ��ӽ�Ŀ
B. ij���Ծ��ϵ�ӡˢ����
C. �ʼ첿�ŶԸ����������ĵ��ʹ�������ĵ���
D. ��ѧ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com