
ЁОЬтФПЁПЕуDЪЧЕШБпЁїABC(МДШ§ЬѕБпЖМЯрЕШЃЌШ§ИіНЧЖМЯрЕШЕФШ§НЧаЮ)БпBAЩЯШЮвтвЛЕу(ЕуDгыЕуBВЛжиКЯ)ЃЌСЌНгDCЃЎ
(1)ШчЭМ1ЃЌвдDCЮЊБпдкBCЩЯЗНзїЕШБпЁїDCFЃЌСЌНгAFЃЌВТЯыЯпЖЮAFгыBDЕФЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЎ
(2)ШчЭМ2ЃЌШєвдDCЮЊБпдкBCЩЯЗНЁЂЯТЗНЗжБ№зїЕШБпЁїDCFКЭЕШБпЁїDCFЁфЃЌСЌНгAFЁЂBFЁфЃЌЬНОПAFЁЂBFЁфгыABгаКЮЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁП(1)BDЃНAFЃЌРэгЩМћНтЮіЃЛ(2)ABЃНAF+BFЁфЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉжЄУїЁїBCDЁеЁїACFЃЌМДПЩЕУГіНсТлЃЛЃЈ2ЃЉжЄУїЁїFЁфCBЁеЁїDCAЃЌЕУЕНBFЁфЃНDAЃЌдйгЩЃЈ1ЃЉМДПЩЕУЕННсТл.
(1)BDЃНAFЃЌ
РэгЩЃКЁпЁїABCКЭЁїDCFЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁрBCЃНACЃЌCDЃНCFЃЌЁЯACBЃНЁЯDCFЃН60ЁуЃЌ
ЁрЁЯBCDЃНЁЯACFЃЌ
дкЁїBCDКЭЁїACFжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїBCDЁеЁїACF(SAS)ЃЌ
ЁрBDЃНAFЃЛ
(2)ABЃНAF+BFЁфЃЌ
РэгЩЃКЁпЁїABCКЭЁїDCFЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁрBCЃНACЃЌCFЁфЃНCDЃЌЁЯFЁфCDЃНЁЯBCAЃН60ЁуЃЌ
ЁрЁЯFЁфCBЃНЁЯDCAЃЌ
дкЁїFЁфCBКЭЁїDCAжаЃЌ
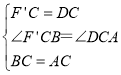 ЃЌ
ЃЌ
ЁрЁїFЁфCBЁеЁїDCA(SAS)ЃЌ
ЁрBFЁфЃНDAЃЌ
гЩ(1)жЊЃЌBDЃНAFЃЌ
ЁпABЃНBD+ADЃЌ
ЁрABЃНAF+BFЁфЃЎ


 УћЪІЕуВІОэЯЕСаД№АИ
УћЪІЕуВІОэЯЕСаД№АИ гЂВХМЦЛЎЦкФЉЕїбаЯЕСаД№АИ
гЂВХМЦЛЎЦкФЉЕїбаЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
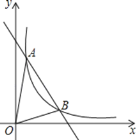
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkx+bгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкAЃЈmЃЌ6ЃЉЃЌBЃЈ3ЃЌnЃЉСНЕуЃЎ
ЕФЭМЯѓНЛгкAЃЈmЃЌ6ЃЉЃЌBЃЈ3ЃЌnЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЭМЯѓжБНгаДГі![]() ЕФxЕФШЁжЕЗЖЮЇЃЛ
ЕФxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЧѓЁїAOBЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЬСЗЯыДгМзЁЂввСНУћдЫЖЏдБжабЁАЮвЛШЫВЮМгЩфЛїНѕБъШќЃЌЙЪЯШдкЩфЛїЖгОйааСЫвЛГЁбЁАЮБШШќЃЎдкЯрЭЌЕФЬѕМўЯТИїЩфАа![]() ДЮЃЌУПДЮЩфАаЕФГЩМЈЧщПіШчЭМЫљЪОЃЎ
ДЮЃЌУПДЮЩфАаЕФГЩМЈЧщПіШчЭМЫљЪОЃЎ
МзЩфАаГЩМЈЕФЬѕаЮЭГМЦЭМ
| ввЩфАаГЩМЈЕФелЯпЭГМЦЭМ
|
ЃЈ![]() ЃЉЧыФуИљОнЭМжаЕФЪ§ОнЬюаДЯТБэЃК
ЃЉЧыФуИљОнЭМжаЕФЪ§ОнЬюаДЯТБэЃК
ЦНОљЪ§ | жкЪ§ | ЗНВю | |
Мз | __________ |
|
|
вв |
| __________ | __________ |
ЃЈ![]() ЃЉИљОнбЁАЮШќНсЙћЃЌНЬСЗбЁдёСЫМздЫЖЏдБВЮМгЩфЛїНѕБъШќЃЌЧыИјГіНтЪЭЃЎ
ЃЉИљОнбЁАЮШќНсЙћЃЌНЬСЗбЁдёСЫМздЫЖЏдБВЮМгЩфЛїНѕБъШќЃЌЧыИјГіНтЪЭЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕ![]() жаЃЌОиаЮ
жаЃЌОиаЮ![]() ЕФ
ЕФ![]() Бпдк
Бпдк![]() жсЩЯЃЌ
жсЩЯЃЌ![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() Бп
Бп![]() ЁЂ
ЁЂ![]() ЕФГЄЗжБ№ЮЊ3ЁЂ8ЃЌ
ЕФГЄЗжБ№ЮЊ3ЁЂ8ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЗДБШР§КЏЪ§
ЕФжаЕуЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЃЌгы
ЃЌгы![]() БпНЛгкЕу
БпНЛгкЕу![]() ЃЎ
ЃЎ
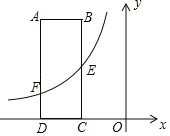
ЃЈ1ЃЉЧѓ![]() ЕФжЕМАОЙ§
ЕФжЕМАОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЕФвЛДЮКЏЪ§ЕФБэДяЪНЃЛ
СНЕуЕФвЛДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШє![]() жсЩЯгавЛЕу
жсЩЯгавЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФжЕзюаЁЃЌЪдЧѓГіЕу
ЕФжЕзюаЁЃЌЪдЧѓГіЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌдкжБЯп
ЃЌдкжБЯп![]() ЩЯеввЛЕу
ЩЯеввЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() жБНгаДГіЗћКЯЬѕМўЕФ
жБНгаДГіЗћКЯЬѕМўЕФ![]() ЕузјБъЃЎ
ЕузјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЙЋЫОЮЊЁАМћвхгТЮЊЛљН№ЛсЁБИїОшПю3000дЊЃЎвбжЊМзЙЋЫОЕФШЫЪ§БШввЙЋЫОЕФШЫЪ§Жр20%ЃЌввЙЋЫОБШМзЙЋЫОШЫОљЖрОш20дЊЃЎЧыФуИљОнЩЯЪіаХЯЂЃЌОЭетСНИіЙЋЫОЕФЁАШЫЪ§ЁБЛђЁАШЫОљОшПюЁБЬсГівЛИігУЗжЪНЗНГЬНтОіЕФЬтЃЌВЂаДГіНтЬтЙ§ГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
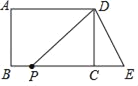
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНаЮABCDжаЃЌABЃН6РхУзЃЌADЃН8РхУзЃЎбгГЄBCЕНЕуEЃЌЪЙCEЃН3РхУзЃЌСЌНгDEЃЎЖЏЕуPДгBЕуГіЗЂЃЌвд2РхУз/УыЕФЫйЖШЯђжеЕуCдШЫйдЫЖЏЃЌСЌНгDPЃЎЩшдЫЖЏЪБМфЮЊtУыЃЌНтД№ЯТСаЮЪЬтЃК
(1)ЕБtЮЊКЮжЕЪБЃЌЁїPCDЮЊЕШбќжБНЧШ§НЧаЮЃП
(2)ЩшЁїPCDЕФУцЛ§ЮЊS(ЦНЗНРхУз)ЃЌЪдШЗЖЈSгыtЕФЙиЯЕЪНЃЛ
(3)ЕБtЮЊКЮжЕЪБЃЌЁїPCDЕФУцЛ§ЮЊГЄЗНаЮABCDУцЛ§ЕФ![]() ЃП
ЃП
(4)ШєЖЏЕуPДгЕуBГіЗЂЃЌвд2РхУз/УыЕФЫйЖШбиBCЉCDЉDAЯђжеЕуAдЫЖЏЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЁїABPКЭЁїDCEШЋЕШЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФвЛдЊЖўДЮЗНГЬx2-x-ЃЈm+1ЃЉ=0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєmЮЊЗћКЯЬѕМўЕФзюаЁећЪ§ЃЌЧѓДЫЗНГЬЕФИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
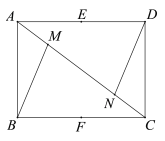
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=3ЃЌBC=4ЃЎMЁЂNдкЖдНЧЯпACЩЯЃЌЧвAM=CNЃЌEЁЂFЗжБ№ЪЧADЁЂBCЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABMЁеЁїCDNЃЛ
ЃЈ2ЃЉЕуGЪЧЖдНЧЯпACЩЯЕФЕуЃЌЁЯEGF=90ЁуЃЌЧѓAGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌEЪЧBCЕФжаЕуЃЌСЌНгAEВЂбгГЄНЛDCЕФбгГЄЯпгкЕуFЃЎ

ЃЈ1ЃЉЧѓжЄЃКAB=CFЃЛ
ЃЈ2ЃЉСЌНгDEЃЌШєAD=2ABЃЌЧѓжЄЃКDEЁЭAFЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com