
【题目】如图,在直角坐标系![]() 中,矩形
中,矩形![]() 的
的![]() 边在
边在![]() 轴上,
轴上,![]() 点坐标为
点坐标为![]() 边
边![]() 、
、![]() 的长分别为3、8,
的长分别为3、8,![]() 是
是![]() 的中点,反比例函数
的中点,反比例函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 边交于点
边交于点![]() .
.
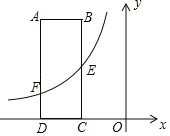
(1)求![]() 的值及经过
的值及经过![]() 、
、![]() 两点的一次函数的表达式;
两点的一次函数的表达式;
(2)若![]() 轴上有一点
轴上有一点![]() ,使
,使![]() 的值最小,试求出点
的值最小,试求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,连接![]() 、
、![]() 、
、![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 直接写出符合条件的
直接写出符合条件的![]() 点坐标.
点坐标.
【答案】(1)k=12,一次函数的表达式为:y=![]() x;(2)P(5,0);(3)(
x;(2)P(5,0);(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)先确定出点B,C坐标,进而得出点E坐标,最后用待定系数法,即可求出直线AE解析式;
(2)先找出点F关于x轴的对称点F'的坐标,进而求出直线EF'的解析式,即可得出结论;
(3)先利用面积和差求出三角形PEF的面积,再求出直线EF的解析式,设出点Q的坐标,过点Q作y轴的平行线交直线EF于G,表示出点G的坐标,利用坐标系中求三角形面积的方法建立方程求解,即可得出结论.
(1)在矩形ABCD中,AB=3,AD=8,
∴CD=AB=3,BC=AD=8,
∵D(6,0),
∴A(6,8),C(3,0),B(3,8),
∵E是BC的中点,
∴E(3,4),
∵点E在反比例函数![]() 的图象上,
的图象上,
∴k=3×4=12,
设经过A、E两点的一次函数的表达式为:y=ax+b,
∴![]() ,解得:
,解得: ,
,
∴经过A.、E两点的一次函数的表达式为:y=![]() x;
x;
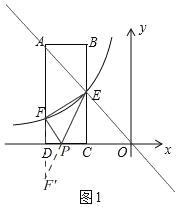
(2)如图1,由(1)可知,k=12,
∴反比例函数的解析式为:![]() ,
,
∵点F的横坐标为6,
∴点F的纵坐标为2,
∴F(6,2),
作点F关于x轴的对称点F′,则F′(6,2),
连接EF′交x轴于P,此时,PE+PF的值最小,
∵E(3,4),
∴由待定系数法可得:直线EF′的解析式为:y=2x+10,
令y=0,则2x+10=0,
∴x=5,
∴P(5,0);
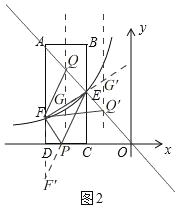
(3)如图2,由(2)知,F′(6,2),
∵E(3,4),F(6,2),
∴S△PEF=S△EFF′S△PFF′=![]() ×(2+2)×(3+6)
×(2+2)×(3+6) ![]() ×(2+2)×(5+6)=4,
×(2+2)×(5+6)=4,
∵E(3,4),F(6,2),
∴由待定系数法得:直线EF的解析式为:y=![]() x+6,
x+6,
由(1)知,经过A.、E两点的一次函数的表达式为:y=![]() x,
x,
设点Q(m,![]() m),
m),
过点Q作y轴的平行线交直线EF于G,
∴G(m,![]() m+6),
m+6),
∴QG=|![]() m
m![]() m6|=|2m+6|,
m6|=|2m+6|,
∵S△QEF=S△PEF,
∴S△QEF=![]() |2m+6|×(3+6)=4,
|2m+6|×(3+6)=4,
∴m=![]() 或m=
或m=![]() ,
,
∴Q(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
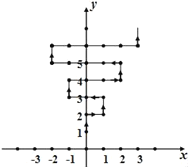
【题目】如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(0,1),(0,2),(1,2),(1,3),(0,3),(﹣1,3)…,根据这个规律探索可得,第90个点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
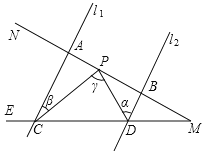
【题目】如图,已知l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)试探索α,β,γ之间有何数量关系?说明理由.
(2)如果BD=3,AB=9,AC=6,并且AC垂直于MN,那么点P运动到什么位置时,△ACP≌△BPD说明理由.
(3)在(2)的条件下,当△ACP≌△BPD时,PC与PD之间有何位置关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
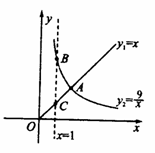
【题目】函数 yl= x ( x ≥0 ) , ![]() ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3 ![]() 时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8
④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y1=![]() 的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)
的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)

(1)求函数y=![]() 和y=kx+b的表达式;
和y=kx+b的表达式;
(2)观察图象,直接写出不等式![]() <kx+b的解.
<kx+b的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点D是等边△ABC(即三条边都相等,三个角都相等的三角形)边BA上任意一点(点D与点B不重合),连接DC.
(1)如图1,以DC为边在BC上方作等边△DCF,连接AF,猜想线段AF与BD的数量关系?请说明理由.
(2)如图2,若以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com