
【题目】如图,已知l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)试探索α,β,γ之间有何数量关系?说明理由.
(2)如果BD=3,AB=9,AC=6,并且AC垂直于MN,那么点P运动到什么位置时,△ACP≌△BPD说明理由.
(3)在(2)的条件下,当△ACP≌△BPD时,PC与PD之间有何位置关系,说明理由.
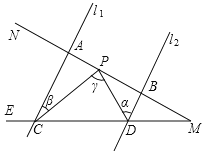
【答案】(1)∠γ=α+∠β;(2)当AP=BD=3,△ACP≌△BPD.(3)CP⊥PD
【解析】
(1)过点P作PF∥l1,根据l1∥l2,可知PF∥l2,故可得出∠α=∠DPF,∠β=∠CPF,由此即可得出结论;
(2)根据平行线的性质得到BD⊥MN,根据全等三角形的性质即可得到结论;
(3)根据全等三角形的性质得到∠ACP=∠DPB,根据垂直的定义即可得到结论.
解:(1)∠γ=α+∠β,
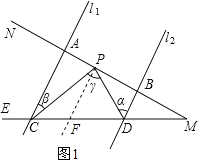
理由:过点P作PF∥l1(如图1),
∵l1∥l2,
∴PF∥l2,
∴∠α=∠DPF,∠β=∠CPF,
∴∠γ=∠DPF+∠CPF=α+∠β;
(2)当AP=BD=3,△ACP≌△BPD,
∵l1∥l2,AC垂直于MN,
∴BD⊥MN,
∴∠CAP=∠PBD=90°,
∵AB=9,
∴PB=6,
∴AC=PB,
在△CAP与△PBD中,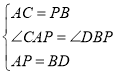 ,
,
∴△ACP≌△BPD,
∴当AP=3时,△ACP≌△BPD;
(3)CP⊥PD,
理由:∵△ACP≌△BPD,
∴∠ACP=∠DPB,
∵∠ACP+∠APC=90°,
∴∠APC+∠DPB=90°,
∴∠CPD=90°,
∴CP⊥PD.


科目:初中数学 来源: 题型:
【题目】已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,则①CA平分∠BCD;②AC⊥BD;③∠ABC=∠ADC=90°;④四边形ABCD的面积为ACBD.上述结论正确的个数是( )

A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教练想从甲、乙两名运动员中选拔一人参加射击锦标赛,故先在射击队举行了一场选拔比赛.在相同的条件下各射靶![]() 次,每次射靶的成绩情况如图所示.
次,每次射靶的成绩情况如图所示.
甲射靶成绩的条形统计图
| 乙射靶成绩的折线统计图
|
(![]() )请你根据图中的数据填写下表:
)请你根据图中的数据填写下表:
平均数 | 众数 | 方差 | |
甲 | __________ |
|
|
乙 |
| __________ | __________ |
(![]() )根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.
)根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
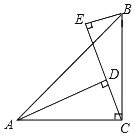
【题目】已知:如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.
(1)求证:△BEC≌△CDA;
(2)当AD=3,BE=1时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
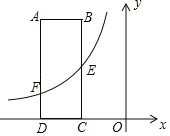
【题目】如图,在直角坐标系![]() 中,矩形
中,矩形![]() 的
的![]() 边在
边在![]() 轴上,
轴上,![]() 点坐标为
点坐标为![]() 边
边![]() 、
、![]() 的长分别为3、8,
的长分别为3、8,![]() 是
是![]() 的中点,反比例函数
的中点,反比例函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 边交于点
边交于点![]() .
.
(1)求![]() 的值及经过
的值及经过![]() 、
、![]() 两点的一次函数的表达式;
两点的一次函数的表达式;
(2)若![]() 轴上有一点
轴上有一点![]() ,使
,使![]() 的值最小,试求出点
的值最小,试求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,连接![]() 、
、![]() 、
、![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 直接写出符合条件的
直接写出符合条件的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
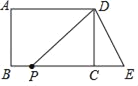
【题目】如图,在长方形ABCD中,AB=6厘米,AD=8厘米.延长BC到点E,使CE=3厘米,连接DE.动点P从B点出发,以2厘米/秒的速度向终点C匀速运动,连接DP.设运动时间为t秒,解答下列问题:
(1)当t为何值时,△PCD为等腰直角三角形?
(2)设△PCD的面积为S(平方厘米),试确定S与t的关系式;
(3)当t为何值时,△PCD的面积为长方形ABCD面积的![]() ?
?
(4)若动点P从点B出发,以2厘米/秒的速度沿BC﹣CD﹣DA向终点A运动,是否存在某一时刻t,使△ABP和△DCE全等?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
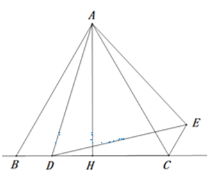
【题目】如图,在![]() 中,
中,![]() ,
,![]() 垂足为
垂足为![]() ,
,![]() 为直线
为直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),在
重合),在![]() 的右侧作
的右侧作![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 在线段
在线段![]() 上时
上时
① 求证:![]() ≌
≌![]() ;
;
② 若![]() , 则
, 则![]() ;
;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com