练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】教练想从甲、乙两名运动员中选拔一人参加射击锦标赛，故先在射击队举行了一场选拔比赛．在相同的条件下各射靶次，每次射靶的成绩情况如图所示．

    甲射靶成绩的条形统计图

    乙射靶成绩的折线统计图

    （）请你根据图中的数据填写下表：

    平均数

    众数

    方差

    甲

    __________

    乙

    __________

    __________

    （）根据选拔赛结果，教练选择了甲运动员参加射击锦标赛，请给出解释．

    【答案】 6 6

    【解析】试题分析：（1）先求出甲射击成绩的平均数，通过观察可得到乙的众数，再根据乙的平均数结合方差公式求出乙射击成绩的方差即可；

    （2）根据平均数和方差的意义，即可得出结果．

    试题解析：（），乙的众数为6，

    ．

    （）因为甲、乙的平均数与众数都相同，甲的方差小，所以更稳定，因此甲的成绩好些．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，CB＝CA，∠ACB＝90°，点D在边BC上(与B，C不重合)，四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC＝FG；②S△FAB∶S四边形CBFG＝1∶2；③∠ABC＝∠ABF；④AD2＝FQ·AC，其中正确结论的个数是(　　)

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在正方形ABCD中，以AB为边向正方形外作等边三角形ABE，连接CE、BD交于点G，连接AG，那么∠AGD的底数是______度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为加强中小学生安全和禁毒教育，某校组织了“防溺水、交通安全、禁毒”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），购买1个足球和1个篮球共需159元；足球单价是篮球单价的2倍少9元．

    （1）求足球和篮球的单价各是多少元？

    （2）根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，学校最多可以购买多少个足球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线顶点D（-1，-4），且过点C（0，-3）.

    （1）求此二次函数的解析式；

    （2）抛物线与x轴交于点A、B，在抛物线上存在一点P使△ABP的面积为10，请直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

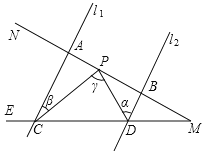
    【题目】如图，已知l1∥l2，射线MN分别和直线l1，l2交于A、B，射线ME分别和直线l1，l2交于C、D，点P在A、B间运动（P与A、B两点不重合），设∠PDB=α，∠PCA=β，∠CPD=γ．

    （1）试探索α，β，γ之间有何数量关系？说明理由．

    （2）如果BD=3，AB=9，AC=6，并且AC垂直于MN，那么点P运动到什么位置时，△ACP≌△BPD说明理由．

    （3）在（2）的条件下，当△ACP≌△BPD时，PC与PD之间有何位置关系，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

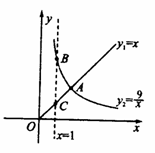
    【题目】函数 yl= x ( x ≥0 ) , （ x > 0 ）的图象如图所示，则结论： ① 两函数图象的交点A的坐标为（3 ,3 ) ② 当 x > 3 时， ③ 当 x ＝1时， BC = 8

    ④ 当 x 逐渐增大时， yl 随着 x 的增大而增大，y2随着 x 的增大而减小．其中正确结论的序号是＿ .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点D是等边△ABC(即三条边都相等，三个角都相等的三角形)边BA上任意一点(点D与点B不重合)，连接DC．

    (1)如图1，以DC为边在BC上方作等边△DCF，连接AF，猜想线段AF与BD的数量关系？请说明理由．

    (2)如图2，若以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′，连接AF、BF′，探究AF、BF′与AB有何数量关系？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图， 是半圆的直径，点是延长线上 一点， 是⊙的切线，切点为，过点作交的延长线于点，连接．求证：

    （）．

    （）．

    查看答案和解析>>

    同步练习册答案