【题目】甲、乙两公司为“见义勇为基金会”各捐款3000元．已知甲公司的人数比乙公司的人数多20%，乙公司比甲公司人均多捐20元．请你根据上述信息，就这两个公司的“人数”或“人均捐款”提出一个用分式方程解决的题，并写出解题过程．
科目：初中数学 来源： 题型：
【题目】在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分拼成一个长方形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（ ）
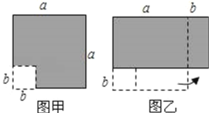
A. （a+2b）（a﹣b）＝a2+ab﹣2b2
B. a2﹣b2＝（a+b）（a﹣b）
C. （a+b）2＝a2+2ab+b2
D. （a﹣b）2＝a2﹣2ab+b2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线顶点D（-1，-4），且过点C（0，-3）.
（1）求此二次函数的解析式；
（2）抛物线与x轴交于点A、B，在抛物线上存在一点P使△ABP的面积为10，请直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
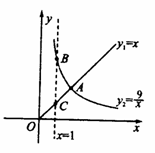
【题目】函数 yl= x ( x ≥0 ) , 
（ x > 0 ）的图象如图所示，则结论： ① 两函数图象的交点A的坐标为（3 ,3 ) ② 当 x > 3 
时， ③ 当 x ＝1时， BC = 8
④ 当 x 逐渐增大时， yl 随着 x 的增大而增大，y2随着 x 的增大而减小．其中正确结论的序号是＿ .
查看答案和解析>>
科目：初中数学 来源： 题型：
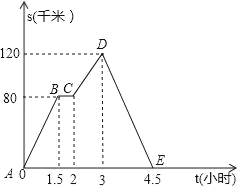
【题目】如下图中的图象(折线ABCDE)描述了一汽车在某一直路上的行驶过程中，汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数关系，根据图中提供的信息，给出下列说法：
①汽车在途中停留了0.5小时；
②汽车行驶3小时后离出发地最远；
③汽车共行驶了120千米；
④汽车返回时的速度是80千米/小时．
其中正确的说法共有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点D是等边△ABC(即三条边都相等，三个角都相等的三角形)边BA上任意一点(点D与点B不重合)，连接DC．
(1)如图1，以DC为边在BC上方作等边△DCF，连接AF，猜想线段AF与BD的数量关系？请说明理由．
(2)如图2，若以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′，连接AF、BF′，探究AF、BF′与AB有何数量关系？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
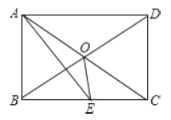
【题目】如图所示，矩形ABCD中，AE平分
交BC于E，
，则下面的结论：①
是等边三角形；②
；③
；④
，其中正确结论有（ ）
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．
(1)、如图①，对△ABC作变换[50°，
]得△AB′C′，则S△AB′C′：S△ABC= ；直线BC与直线B′C′所夹的锐角为 度；
(2)、如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB'C'，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；
(3)、如图③，△ABC中，AB=AC，∠BAC=36°，BC=l，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ和n的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙
半径为
， 
是⊙
的直径，点
为
延长线上一点，动点
从点
出发以
的速度沿
方向运动，同时，动点
从点
出发以
的速度沿
方向运动，当两点相遇时都停止运动．过点
作
的垂线，与⊙
分别交于点
、
，设点
的运动时间为
．
（
）当四边形
是正方形时， 
__________ 
， 
__________ 
．
（
）当四边形
是菱形且
时，求
内切圆的半径．
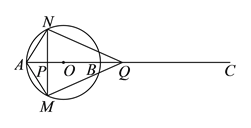
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
