
【题目】(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的![]() .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的![]() ,求道路的宽.
,求道路的宽.

【答案】(1)道路宽为2米;(2)道路的宽为1米.
【解析】试题分析:(1)设道路宽为x米,利用平移把不规则的图形变为规则图形,如此一来,所有草坪面积之和就变为了(20﹣x)(12﹣x)米2,进而即可列出方程,求出答案;
(2)设道路的宽为x米,则正方形边长为4x,根据道路与观赏亭的面积之和是矩形面积的![]() ,列方程求解即可.
,列方程求解即可.
试题解析:解:(1)设道路宽为x米,
根据题意得:(20﹣x)(12﹣x)=180
解得:x1=30(舍去),x2=2
答:道路宽为2米;
(2)设道路的宽为x米,
则可列方程:x(12-4x)+x(20-4x)+16x2=![]() ×20×12,
×20×12,
即:x2+4x-5=0,
解得:x1=1,x2=-5(舍去),
答:道路的宽为1米.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
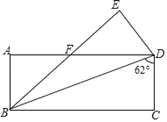
【题目】如图,将长方形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
A. 62°B. 56°C. 31°D. 28°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2+2x+c与直线y2=kx+b交于点A(-1,0)、B(2,3).
(1)求a、b、c的值;
(2)直接写出当y1<y2时,自变量的范围是__________________________.
(3)若点C是抛物线的顶点,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC延长线于F,且垂足为E,则下列结论:①AD=BF;②∠BAE=∠FBC;③S△ADB=S△ADC;④AC+CD=AB;⑤AD=2BE.其中正确的结论有______(填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索题:(x-1)((x+1)=x2-1,
(x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1,
(x-1)(x4+x3+x2+x+1)=x5-1.
(1)观察以上各式并猜想:
①(x-1)(x6+x5+x4+x3+x2+x+1)=________________________;
②(x-1)(xn+xn-1+xn-2+…+x3+x2+x+1)= ________________________;
(2)请利用上面的结论计算:
①(-2)50+(-2)49+(-2)48+…+(-2)+1
②若x1007+x1006+…+x3+x2+x+1=0,求x2016的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1,x2.
(1)求m的取值范围.
(2)若|x1|=|x2|,求m的值及方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市公共自行车服务公司调查某中学学生对公共自行车的了解情况,随机抽取部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图.

(1)本次问卷共随机调查了 名学生,扇形统计图中![]() .
.
(2)请根据数据信息补全条形统计图,并求扇形统计图中“D类型”所对应的圆心角.
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com