
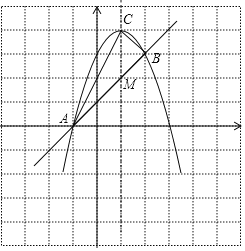
【题目】已知抛物线y1=ax2+2x+c与直线y2=kx+b交于点A(-1,0)、B(2,3).
(1)求a、b、c的值;
(2)直接写出当y1<y2时,自变量的范围是__________________________.
(3)若点C是抛物线的顶点,求△ABC的面积.
【答案】![]()
【解析】试题分析:(1)利用待定系数法即可求得;
(2)判断抛物线的开口,根据交点坐标即可求得;
(3)先利用配方法求出抛物线的顶点![]() 的坐标,设对称轴与直线
的坐标,设对称轴与直线![]() 交于点
交于点![]() ,求出
,求出![]() 那么
那么![]() 再根据
再根据![]() 即可求解.
即可求解.
试题解析:(1)∵抛物线![]() 与直线
与直线![]() 交于点A(1,0)、B(2,3).
交于点A(1,0)、B(2,3).
![]()
![]()
解得![]()
![]()
∴a=1,b=1,c=3;
(2) ![]()
∴抛物线的开口向下,
∴x<1或x>2时,抛物线上的部分在直线的下方,
∴当y1<y2时,自变量的范围是x<1或x>2.
故答案为x<1或x>2;
(3) ![]()
∴抛物线的顶点C的坐标为(1,4).
设对称轴与直线![]() 交于点M,
交于点M,
∵当x=1时,y=1+1=2,
∴M(1,2),
∴CM=42=2,
∵A(1,0),B(2,3),
![]()


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
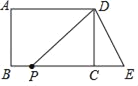
【题目】如图,在长方形ABCD中,AB=6厘米,AD=8厘米.延长BC到点E,使CE=3厘米,连接DE.动点P从B点出发,以2厘米/秒的速度向终点C匀速运动,连接DP.设运动时间为t秒,解答下列问题:
(1)当t为何值时,△PCD为等腰直角三角形?
(2)设△PCD的面积为S(平方厘米),试确定S与t的关系式;
(3)当t为何值时,△PCD的面积为长方形ABCD面积的![]() ?
?
(4)若动点P从点B出发,以2厘米/秒的速度沿BC﹣CD﹣DA向终点A运动,是否存在某一时刻t,使△ABP和△DCE全等?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 垂足为
垂足为![]() ,
,![]() 为直线
为直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),在
重合),在![]() 的右侧作
的右侧作![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 在线段
在线段![]() 上时
上时
① 求证:![]() ≌
≌![]() ;
;
② 若![]() , 则
, 则![]() ;
;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是圆弧形拱桥,某天测得水面![]() 宽
宽![]() ,此时圆弧最高点距水面
,此时圆弧最高点距水面![]() .
.
(![]() )确定圆弧所在圆的圆心
)确定圆弧所在圆的圆心![]() .(尺规作图,保留作图痕迹)
.(尺规作图,保留作图痕迹)
(![]() )求圆弧所在圆的半径.
)求圆弧所在圆的半径.
(![]() )水面上升
)水面上升![]() ,水面宽__________
,水面宽__________ ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为点B(0,3),其顶点为C,对称轴为x=1,
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S,并求其最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别在钱段AB、AC上,CD与BE交于O,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD

A. ∠B=∠CB. AD=AEC. BE=CDD. BD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的![]() .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的![]() ,求道路的宽.
,求道路的宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
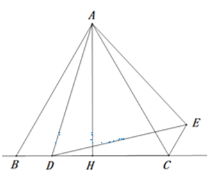
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B. C重合),以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC.设∠BAC=α,∠BCE=β.

(1)如图1,如果∠BAC=90,∠BCE=___度;
(2)如图2,你认为α、β之间有怎样的数量关系?并说明理由。
(3)当点D在线段BC的延长线上移动时,α、β之间又有怎样的数量关系?请在备用图上画出图形,并直接写出你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com