
【题目】如图,AB是半圆O的直径,C是半圆O上一点(不与点A、B重合),D是![]() 的中点,DE⊥AB于点E,过点C作半圆O的切线,交ED的延长线于点F.
的中点,DE⊥AB于点E,过点C作半圆O的切线,交ED的延长线于点F.
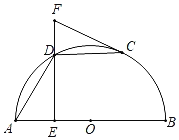
(1)求证:∠FCD=∠ADE;
(2)填空:
①当∠FCD的度数为 时,四边形OADC是菱形;
②若AB=2![]() ,当CF∥AB时,DF的长为 .
,当CF∥AB时,DF的长为 .
【答案】(1)见解析;(2)①30°;②![]() ﹣1.
﹣1.
【解析】
(1)如下图,先推导出∠OAD=∠OCD,然后再利用CF⊥OC和DE⊥AB进行角度转化,推导出∠FCD=∠ADE;
(2)①当∠FCD=30°时,可得到△OAD是等边三角形,然后再推导出△COD也是等边三角形,从而证菱形;
②如下图,先证△ADE≌△DCF,得出AE=DF,DE=CF,推导出△ODE是等腰直角三角形,从而求出DF的长.
(1)证明:连接OC、AC.如图1所示:
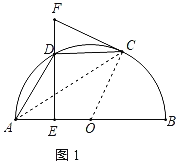
∵D是![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴DA=DC,
∴∠DAC=∠DCA.
∵OA=OC,
∴∠OAC=∠OCA.
∴∠DAC+∠OAC=∠DCA+∠OCA,
即∠OAD=∠OCD.
∵CF是半圆O的切线,
∴CF⊥OC,
∴∠FCD+∠OCD=90°,
∵DE⊥AB,
∴∠ADE+∠OAD=90°,
∴∠FCD=∠ADE.
(2)解:①当∠FCD的度数为30°时,四边形OADC是菱形;理由如下:
连接OD,如图2所示:
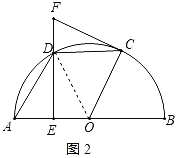
∵∠FCD=30°,
∴∠ADE=30°,
∵DE⊥AB,
∴∠OAD=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OA,∠AOD=60°,
∵D是![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴∠AOD=∠COD=60°,
∵OC=OD,
∴△COD是等边三角形,
∴CD=OD=OC,
∴OA=AD=CD=OC,
∴四边形OADC是菱形;
故答案为:30°;
②连接OD,如图3所示:
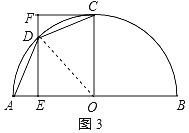
∵AB=2![]() ,
,
∴OA=OD=![]() ,
,
∵CF∥AB,DE⊥AB,
∴CF⊥EF,
∴∠CFD=90°=∠DEA,
在△ADE和△DCF中,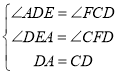 ,
,
∴△ADE≌△DCF(AAS),
∴AE=DF,DE=CF,
∵CF半圆O的切线,
∴CF⊥OC,
∴四边形OCFE是矩形,
∴CF=OE,
∴DE=OE,
∴△ODE是等腰直角三角形,
∴OE=![]() OD=1,
OD=1,
∴DF=AE=OA﹣OE=![]() ﹣1;
﹣1;
故答案为:![]() ﹣1.
﹣1.


科目:初中数学 来源: 题型:
【题目】为了运送防疫物资,甲、乙两货运公司各派出一辆卡车,分别从距目的地240千米和270千米的两地同时出发,驰援疫区.已知乙公司卡车的平均速度是甲公司卡车的平均速度的1.5倍,甲公司的卡车比乙公司的卡车晚1小时到达目的地,分别求甲、乙两货运公司卡车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接体育理化加试,九(2)班同学到某体育用品商店采购训练用球,已知购买3个A品牌足球和2个B品牌足球需付210元;购买2个A品牌足球和1个B品牌足球需付费130元.(优惠措施见海报)

(1)求A,B两品牌足球的单价各为多少元;
(2)为享受优惠,同学们决定购买一次性购买足球60个,若要求A品牌足球的数量不低于B品牌足球数量的3倍,请你设计一种付费最少的方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
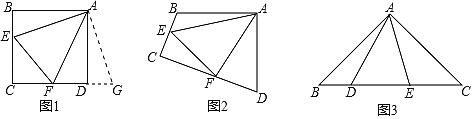
【题目】探究:如图1和图2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
(1)①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系 ;
②如图2,若∠B、∠D都不是直角,但满足∠B+∠D=180°,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2![]() .点D、E均在边BC边上,且∠DAE=45°,若BD=1,求DE的长.
.点D、E均在边BC边上,且∠DAE=45°,若BD=1,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
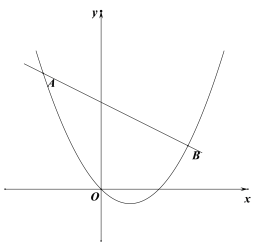
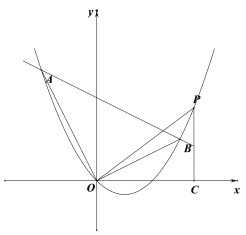
(1)求抛物线的解析式.
(2)在直线![]() 下方的抛物线上求点
下方的抛物线上求点![]() ,求
,求![]() 的面积等于20.
的面积等于20.
(3)若![]() 在抛物线上,作
在抛物线上,作![]() 轴于点
轴于点![]() ,若
,若![]() 和
和![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+c交x轴于点A(3,0),交y轴于点B,抛物线y=﹣x2+bx+c经过点A,B.
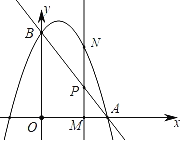
(1)求抛物线的解析式;
(2)点M(m,0)是线段OA上一动点(点M不与点O,A重合),过点M作y轴的平行线,交直线AB于点P,交抛物线于点N,若NP=![]() AP,求m的值;
AP,求m的值;
(3)若抛物线上存在点Q,使∠QBA=45°,请直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2.
x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2.
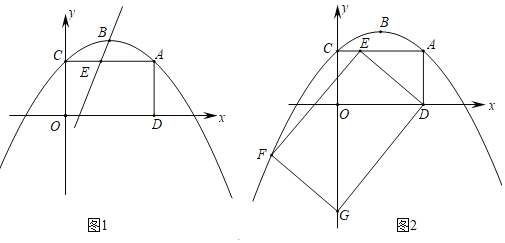
(1)求抛物线的函数表达式和顶点B的坐标;
(2)如图1,抛物线与y轴交于点C,连接AC,过A作AD⊥x轴于点D,E是线段AC上的动点(点E不与A,C两点重合);
(i)若直线BE将四边形ACOD分成面积比为1:3的两部分,求点E的坐标;
(ii)如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在y轴上的同时点F恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
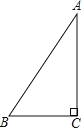
【题目】如图,已知Rt△ABC中∠C=90°,AB=10,AC=8.
(1)作AB的垂直平分线DE,交AB于点D,交AC于点E.(要求尺规作图,不写作法,保留作图痕迹);
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为稳步推进5G网络建设,深化共建共享,当甲队施工20天完成5G基站建设工程的![]() 时,乙队加入该工程,结果比甲队单独施工提前25天完成了剩余的工程.
时,乙队加入该工程,结果比甲队单独施工提前25天完成了剩余的工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若乙队参与该项工程施工的时间不超过12天,则甲队从开始施工到完成该工程至少需要多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com