
ΓΨΧβΡΩΓΩΈΣΝΥ”≠Ϋ”Χε”ΐάμΜ·Φ” ‘Θ§Ψ≈Θ®2Θ©ΑύΆ§―ßΒΫΡ≥Χε”ΐ”ΟΤΖ…ΧΒξ≤…ΙΚ―ΒΝΖ”Ο«ρΘ§“―÷ΣΙΚ¬ρ3ΗωAΤΖ≈ΤΉψ«ρΚΆ2ΗωBΤΖ≈ΤΉψ«ρ–ηΗΕ210‘ΣΘΜΙΚ¬ρ2ΗωAΤΖ≈ΤΉψ«ρΚΆ1ΗωBΤΖ≈ΤΉψ«ρ–ηΗΕΖ―130‘ΣΘ°Θ®”≈Μί¥κ ©ΦϊΚΘ±®Θ©

Θ®1Θ©«σAΘ§BΝΫΤΖ≈ΤΉψ«ρΒΡΒΞΦέΗςΈΣΕύ…Ό‘ΣΘΜ
Θ®2Θ©ΈΣœμ ή”≈ΜίΘ§Ά§―ßΟ«ΨωΕ®ΙΚ¬ρ“Μ¥Έ–‘ΙΚ¬ρΉψ«ρ60ΗωΘ§»τ“Σ«σAΤΖ≈ΤΉψ«ρΒΡ ΐΝΩ≤ΜΒΆ”ΎBΤΖ≈ΤΉψ«ρ ΐΝΩΒΡ3±ΕΘ§«κΡψ…ηΦΤ“Μ÷÷ΗΕΖ―Ήν…ΌΒΡΖΫΑΗΘ§≤ΔΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©AΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣ50‘ΣΘ§BΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣ30‘ΣΘΜΘ®2Θ©ΙΚ¬ρAΤΖ≈ΤΉψ«ρ45ΗωΘ§BΤΖ≈ΤΉψ«ρ15ΗωΜ®Ζ―Ήν…ΌΘ§Ήν…ΌΖ―”ΟΈΣ2250‘ΣΘ§άμ”…ΦϊΫβΈωΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηAΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣx‘ΣΘ§BΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣy‘ΣΘ§ΗυΨίΙΚ¬ρ3ΗωAΤΖ≈ΤΉψ«ρΚΆ2ΗωBΤΖ≈ΤΉψ«ρ–ηΗΕ210‘ΣΘΜΙΚ¬ρ2ΗωAΤΖ≈ΤΉψ«ρΚΆ1ΗωBΤΖ≈ΤΉψ«ρ–ηΗΕΖ―130‘ΣΝ–ΖΫ≥ΧΉι«σΫβΩ…ΒΟΘΜ
Θ®2Θ©…ηΙΚ¬ρAΤΖ≈ΤΉψ«ρΈΣaΗωΘ§‘ρΙΚ¬ρBΤΖ≈ΤΉψ«ρΈΣΘ®60©¹aΘ©ΗωΘ§ΗυΨίAΤΖ≈ΤΉψ«ρΒΡ ΐΝΩ≤ΜΒΆ”ΎBΤΖ≈ΤΉψ«ρ ΐΝΩΒΡ3±ΕΝ–“Μ‘Σ“Μ¥Έ≤ΜΒ» Ϋ«σΫβΘ§»ΜΚσΗυΨίΧβ“β±μ Ψ≥ωΙΚ¬ρΉήΖ―”ΟW”κaΒΡΚ· ΐΙΊœΒ ΫΘ§»ΜΚσΗυΨί“Μ¥ΈΚ· ΐΆΦœώ–‘÷ Ζ÷ΈωΉν÷ΒΘ°
ΫβΘΚΘ®1Θ©…ηAΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣx‘ΣΘ§BΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣy‘ΣΘ§ΗυΨίΧβ“βΒΟΘΚ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§¥πΘΚAΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣ50‘ΣΘ§BΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣ30‘ΣΘΜ
Θ§¥πΘΚAΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣ50‘ΣΘ§BΤΖ≈ΤΉψ«ρΒΡΒΞΦέΈΣ30‘ΣΘΜ
Θ®2Θ©…ηΙΚ¬ρAΤΖ≈ΤΉψ«ρΈΣaΗωΘ§‘ρΙΚ¬ρBΤΖ≈ΤΉψ«ρΈΣΘ®60©¹aΘ©ΗωΘ§ΗυΨίΧβ“βΒΟΘΚ
![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§Ι AΤΖ≈ΤΉψ«ρΩ…œμ8’έΘ§BΤΖ≈ΤΉψ«ρ‘≠ΦέΘΜ
Θ§Ι AΤΖ≈ΤΉψ«ρΩ…œμ8’έΘ§BΤΖ≈ΤΉψ«ρ‘≠ΦέΘΜ
…ηΙΚ¬ρAΘ§BΝΫΤΖ≈ΤΉψ«ρΒΡΉήΖ―”ΟΈΣW‘ΣΘ§
‘ρWΘΫ0Θ°8ΓΝ50a+30Θ®60©¹aΘ©ΘΫ10a+1800Θ§
ΓΏkΘΫ10ΘΨ0Θ§ΓύWΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§
ΓύΒ±aΘΫ45 ±Θ§Μ®Ζ―Ήν…ΌΘ§Ήν…ΌΖ―”ΟΈΣΘΚ10ΓΝ45+1800ΘΫ2250Θ®‘ΣΘ©Θ°
¥πΘΚΙΚ¬ρAΤΖ≈ΤΉψ«ρ45ΗωΘ§BΤΖ≈ΤΉψ«ρ15ΗωΜ®Ζ―Ήν…ΌΘ§Ήν…ΌΖ―”ΟΈΣ2250‘ΣΘ°


 ΩΎΥψ–ΡΥψΥΌΥψ”Π”ΟΧβœΒΝ–¥πΑΗ
ΩΎΥψ–ΡΥψΥΌΥψ”Π”ΟΧβœΒΝ–¥πΑΗ Ά§≤ΫΆΊ’Ι‘ΡΕΝœΒΝ–¥πΑΗ
Ά§≤ΫΆΊ’Ι‘ΡΕΝœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=![]() x2+bxΘ≠2”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎCΒψΘ§«“AΘ®“Μ1Θ§0Θ©Θ°
x2+bxΘ≠2”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎCΒψΘ§«“AΘ®“Μ1Θ§0Θ©Θ°

Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΦΑΕΞΒψDΒΡΉχ±ξΘΜ
Θ®2Θ©≈–ΕœΓςABCΒΡ–ΈΉ¥Θ§÷ΛΟςΡψΒΡΫα¬έΘΜ
Θ®3Θ©ΒψM «x÷α…œΒΡ“ΜΗωΕ·ΒψΘ§Β±ΓςDCMΒΡ÷ή≥ΛΉν–Γ ±Θ§«σΒψMΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Α―“ΜΩιΚ§30ΓψΫ«ΒΡ»ΐΫ«ΑεΒΡ÷±Ϋ«ΕΞΒψΖ≈‘ΎΖ¥±»άΐΚ· ΐy=-![]() Θ®xΘΦ0Θ©ΒΡΆΦœσ…œΒΡΒψC¥ΠΘ§ΝμΝΫΗωΕΞΒψΖ÷±π¬δ‘Ύ‘≠ΒψOΚΆx÷αΒΡΗΚΑκ÷α…œΒΡΒψA¥ΠΘ§«“ΓœCAO=30ΓψΘ§‘ρAC±Ώ”κΗΟΚ· ΐΆΦœσΒΡΝμ“ΜΫΜΒψDΒΡΉχ±ξΈΣ__________Θ°
Θ®xΘΦ0Θ©ΒΡΆΦœσ…œΒΡΒψC¥ΠΘ§ΝμΝΫΗωΕΞΒψΖ÷±π¬δ‘Ύ‘≠ΒψOΚΆx÷αΒΡΗΚΑκ÷α…œΒΡΒψA¥ΠΘ§«“ΓœCAO=30ΓψΘ§‘ρAC±Ώ”κΗΟΚ· ΐΆΦœσΒΡΝμ“ΜΫΜΒψDΒΡΉχ±ξΈΣ__________Θ°
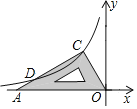
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓςABCΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΒψOΈΣAB±Ώ…œ“ΜΒψΘ§«“BO=2AO=4Θ§ΫΪΓςABC»ΤΒψOΡφ ±’κ–ΐΉΣ60ΓψΒΟΓςDEFΘ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣ______Θ°
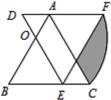
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2020Ρξ3‘¬24»’Θ§ΙΛ–≈≤ΩΖΔ≤ΦΓΕΙΊ”ΎΆΤΕ·![]() Φ”ΩλΖΔ’ΙΒΡΆ®÷ΣΓΖΘ§»ΪΝΠΆΤΫχ
Φ”ΩλΖΔ’ΙΒΡΆ®÷ΣΓΖΘ§»ΪΝΠΆΤΫχ![]() Άχ¬γΫ®…ηΓΔ”Π”ΟΆΤΙψΓΔΦΦ θΖΔ’ΙΚΆΑ≤»Ϊ±Θ’œΘ°ΙΛ–≈≤ΩΧα≥ωΘ§“Σ≈ύ”ΐ–¬–ΆœϊΖ―ΡΘ ΫΘ§Φ”Ωλ”ΟΜßœρ
Άχ¬γΫ®…ηΓΔ”Π”ΟΆΤΙψΓΔΦΦ θΖΔ’ΙΚΆΑ≤»Ϊ±Θ’œΘ°ΙΛ–≈≤ΩΧα≥ωΘ§“Σ≈ύ”ΐ–¬–ΆœϊΖ―ΡΘ ΫΘ§Φ”Ωλ”ΟΜßœρ![]() «®“ΤΘ§ΆΤΕ·ΓΑ
«®“ΤΘ§ΆΤΕ·ΓΑ![]() “ΫΝΤΫΓΩΒΓ±¥¥–¬ΖΔ’ΙΘ§ Β ©ΓΑ
“ΫΝΤΫΓΩΒΓ±¥¥–¬ΖΔ’ΙΘ§ Β ©ΓΑ![]() ΙΛ“ΒΜΞΝΣΆχΓ±512ΙΛ≥ΧΘ§¥ΌΫχΓΑ
ΙΛ“ΒΜΞΝΣΆχΓ±512ΙΛ≥ΧΘ§¥ΌΫχΓΑ![]() ≥ΒΝΣΆχΓ±–≠Ά§ΖΔ’ΙΘ§ΙΙΫ®
≥ΒΝΣΆχΓ±–≠Ά§ΖΔ’ΙΘ§ΙΙΫ®![]() ”Π”Ο…ζΧ§œΒΆ≥Θ°œ÷ΓΑ
”Π”Ο…ζΧ§œΒΆ≥Θ°œ÷ΓΑ![]() Άχ¬γΓ±“―≥…ΈΣ“ΜΗω»»Ο≈¥ ΜψΘ§Ρ≥–ΘΈΣΝΥΫβΨ≈ΡξΦΕ―ß…ζΕ‘ΓΑ
Άχ¬γΓ±“―≥…ΈΣ“ΜΗω»»Ο≈¥ ΜψΘ§Ρ≥–ΘΈΣΝΥΫβΨ≈ΡξΦΕ―ß…ζΕ‘ΓΑ![]() Άχ¬γΓ±ΒΡΝΥΫβ≥ΧΕ»Θ§Ε‘Ψ≈ΡξΦΕ―ß…ζ––ΝΥ“Μ¥Έ≤β ‘(“ΜΙ≤10ΒάΧβ¥πΕ‘1ΒάΒΟ1Ζ÷Θ§¬ζΖ÷10Ζ÷)Θ§≤β ‘Ϋα χΚσΥφΜζ≥ι»ΓΝΥ≤ΩΖ÷―ß…ζΒΡ≥…Φ®’ϊάμΖ÷ΈωΘ§Μφ÷Τ≥ω»γΆΦΥυ ΨΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΗυΨίΆΦ÷––≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Άχ¬γΓ±ΒΡΝΥΫβ≥ΧΕ»Θ§Ε‘Ψ≈ΡξΦΕ―ß…ζ––ΝΥ“Μ¥Έ≤β ‘(“ΜΙ≤10ΒάΧβ¥πΕ‘1ΒάΒΟ1Ζ÷Θ§¬ζΖ÷10Ζ÷)Θ§≤β ‘Ϋα χΚσΥφΜζ≥ι»ΓΝΥ≤ΩΖ÷―ß…ζΒΡ≥…Φ®’ϊάμΖ÷ΈωΘ§Μφ÷Τ≥ω»γΆΦΥυ ΨΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΗυΨίΆΦ÷––≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
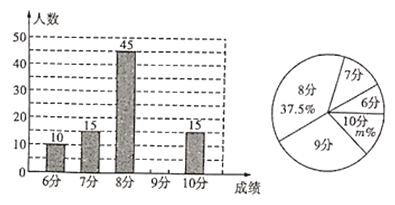
Θ®1Θ©«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘ§…»–ΈΆ≥ΦΤΆΦ÷–![]() ΓΓΓΓΓΓΓΓ__ΘΜ
ΓΓΓΓΓΓΓΓ__ΘΜ
Θ®2Θ©ΥυΒς≤ι―ß…ζ≥…Φ®ΒΡ÷Ύ ΐ «_ΓΓΓΓΓΓΓΓ____Ζ÷Θ§ΤΫΨυ ΐ «_ΓΓΓΓΓΓΓΓΖ÷ΘΜ
Θ®3Θ©»τΗΟ–ΘΨ≈ΡξΦΕ―ß…ζ”–![]() »ΥΘ§«κΙάΦΤΒΟΖ÷≤Μ…Ό”Ύ
»ΥΘ§«κΙάΦΤΒΟΖ÷≤Μ…Ό”Ύ![]() Ζ÷ΒΡ”–Εύ…Ό»ΥΘΩ
Ζ÷ΒΡ”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy1=ax2+bx+cΘ®aΓΌ0Θ©ΒΡΕΞΒψΉχ±ξAΘ®©¹1Θ§3Θ©Θ§”κx÷αΒΡ“ΜΗωΫΜΒψBΘ®©¹4Θ§0Θ©Θ§÷±œΏy2=mx+nΘ®mΓΌ0Θ©”κ≈ΉΈοœΏΫΜ”ΎAΘ§BΝΫΒψΘ§œ¬Ν–Ϋα¬έΘΚΔΌ2a©¹b=0ΘΜΔΎabcΘΦ0ΘΜΔέ≈ΉΈοœΏ”κx÷αΒΡΝμ“ΜΗωΫΜΒψΉχ±ξ «Θ®3Θ§0Θ©ΘΜΔήΖΫ≥Χax2+bx+c©¹3=0”–ΝΫΗωœύΒ»ΒΡ Β ΐΗυΘΜΔίΒ±©¹4ΘΦxΘΦ©¹1 ±Θ§‘ρy2ΘΦy1Θ°
Τδ÷–’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©

A. ΔΌΔΎΔέ B. ΔΌΔέΔί C. ΔΌΔήΔί D. ΔΎΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Ακ‘≤OΒΡ÷±ΨΕΘ§C «Ακ‘≤O…œ“ΜΒψΘ®≤Μ”κΒψAΓΔB÷ΊΚœΘ©Θ§D «![]() ΒΡ÷–ΒψΘ§DEΓΆAB”ΎΒψEΘ§ΙΐΒψCΉςΑκ‘≤OΒΡ«–œΏΘ§ΫΜEDΒΡ―”≥ΛœΏ”ΎΒψFΘ°
ΒΡ÷–ΒψΘ§DEΓΆAB”ΎΒψEΘ§ΙΐΒψCΉςΑκ‘≤OΒΡ«–œΏΘ§ΫΜEDΒΡ―”≥ΛœΏ”ΎΒψFΘ°
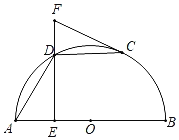
Θ®1Θ©«σ÷ΛΘΚΓœFCDΘΫΓœADEΘΜ
Θ®2Θ©ΧνΩ’ΘΚ
ΔΌΒ±ΓœFCDΒΡΕ» ΐΈΣΓΓ ΓΓ ±Θ§ΥΡ±Ώ–ΈOADC «Νβ–ΈΘΜ
ΔΎ»τABΘΫ2![]() Θ§Β±CFΓΈAB ±Θ§DFΒΡ≥ΛΈΣΓΓ ΓΓΘ°
Θ§Β±CFΓΈAB ±Θ§DFΒΡ≥ΛΈΣΓΓ ΓΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣ¬ζΉψ –≥Γ–η«σΘ§Ρ≥≥§ –‘Ύ÷–«οΫΎά¥ΝΌ«ΑœΠΘ§ΙΚΫχ“Μ÷÷ΤΖ≈Τ‘¬±ΐΘ§ΟΩΚ–ΫχΦέ «40‘ΣΘ§≥§ –ΙφΕ®ΟΩΚ– έΦέ≤ΜΒΟ…Ό”Ύ45‘ΣΘ§ΗυΨί“‘Άυœζ έΨ≠―ιΖΔœ÷ΘΚΒ± έΦέΕ®ΈΣΟΩΚ–45‘Σ ±Θ§ΟΩΧλΩ…“‘¬τ≥ω700Κ–Θ§ΟΩΚ– έΦέΟΩΧαΗΏ1‘ΣΘ§ΟΩΧλ“Σ…Ό¬τ≥ω20Κ–Θ°
Θ®1Θ©«κ–¥≥ωΟΩΧλΒΡœζ έάϊ»σ![]() Θ®‘ΣΘ©”κΟΩΚ–’«Φέ
Θ®‘ΣΘ©”κΟΩΚ–’«Φέ![]() Θ®‘ΣΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΦΑΉ‘±δΝΩ
Θ®‘ΣΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΦΑΉ‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©Β±ΟΩΚ–’«ΦέΈΣΕύ…Ό‘Σ ±Θ§ΟΩΧλΒΡœζ έάϊ»σ![]() Ήν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
Ήν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
Θ®3Θ©»γΙϊ≥§ –œκ“ΣΟΩΧλΜώΒΟ≤ΜΒΆ”Ύ6000‘ΣΒΡάϊ»σΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com