
°Њћвƒњ°њќ™¬ъ„г –≥°–и«у£ђƒ≥≥ђ –‘Џ÷–«пљЏјіЅў«∞ѕ¶£ђєЇљш“ї÷÷∆Ј≈∆‘¬±э£ђ√њЇ–љшЉџ «40‘™£ђ≥ђ –єжґ®√њЇ– џЉџ≤їµ√…ў”Џ45‘™£ђЄщЊЁ“‘Ќщѕъ џЊ≠—йЈҐѕ÷£Їµ± џЉџґ®ќ™√њЇ–45‘™ ±£ђ√њћмњ…“‘¬ф≥ц700Ї–£ђ√њЇ– џЉџ√њћбЄя1‘™£ђ√њћм“™…ў¬ф≥ц20Ї–£Ѓ
£®1£©«л–і≥ц√њћмµƒѕъ џјы»у![]() £®‘™£©”л√њЇ–’«Љџ
£®‘™£©”л√њЇ–’«Љџ![]() £®‘™£©÷ЃЉдµƒЇѓ эєЎѕµ љЉ∞„‘±дЅњ
£®‘™£©÷ЃЉдµƒЇѓ эєЎѕµ љЉ∞„‘±дЅњ![]() µƒ»°÷µЈґќІ£ї
µƒ»°÷µЈґќІ£ї
£®2£©µ±√њЇ–’«Љџќ™ґа…ў‘™ ±£ђ√њћмµƒѕъ џјы»у![]() „оіу£њ„оіујы»у «ґа…ў£њ
„оіу£њ„оіујы»у «ґа…ў£њ
£®3£©»зєы≥ђ –ѕл“™√њћмїсµ√≤їµЌ”Џ6000‘™µƒјы»у£ђ«у![]() µƒ»°÷µЈґќІ£Ѓ
µƒ»°÷µЈґќІ£Ѓ
°Њір∞Є°њ£®1£©![]() =-20x2+600x+3500,
=-20x2+600x+3500, ![]() £ї£®2£©µ±√њЇ–’«Љџќ™15‘™ ±£ђ√њћмµƒѕъ џјы»у
£ї£®2£©µ±√њЇ–’«Љџќ™15‘™ ±£ђ√њћмµƒѕъ џјы»у![]() „оіу£ђ„оіујы»у «8000‘™£ї£®3£©µ±5°№x°№25 ±£ђ≥ђ –ѕл“™√њћмїсµ√≤їµЌ”Џ6000‘™µƒјы»у
„оіу£ђ„оіујы»у «8000‘™£ї£®3£©µ±5°№x°№25 ±£ђ≥ђ –ѕл“™√њћмїсµ√≤їµЌ”Џ6000‘™µƒјы»у
°Њљвќц°њ
£®1£©ЄщЊЁ°∞ѕъ џјы»у=√њЇ–µƒјы»у°ЅЇ– э°±Љіњ…«у≥ц√њћмµƒѕъ џјы»у![]() £®‘™£©”л√њЇ–’«Љџ
£®‘™£©”л√њЇ–’«Љџ![]() £®‘™£©÷ЃЉдµƒЇѓ эєЎѕµ љ£ђ»їЇуЄщЊЁћв“вЉіњ…«у≥цxµƒ»°÷µЈґќІ£ї
£®‘™£©÷ЃЉдµƒЇѓ эєЎѕµ љ£ђ»їЇуЄщЊЁћв“вЉіњ…«у≥цxµƒ»°÷µЈґќІ£ї
£®2£©љЂ£®1£©÷–ґюіќЇѓ эµƒ“ї∞г љ„™їѓќ™ґ•µг љЉіњ…«у≥ц![]() µƒ„о÷µ£ї
µƒ„о÷µ£ї
£®3£©ѕ»«у≥цµ±![]() =6000 ±£ђxµƒ÷µ£ђ»їЇујы”√ґюіќЇѓ эµƒњ™њЏЈљѕтЉіњ…µ√≥цљб¬џ£Ѓ
=6000 ±£ђxµƒ÷µ£ђ»їЇујы”√ґюіќЇѓ эµƒњ™њЏЈљѕтЉіњ…µ√≥цљб¬џ£Ѓ
љв£Ї£®1£©ЄщЊЁћв“вњ…µ√£Ї![]() =£®45£Ђx£≠40£©£®700£≠20x£©=-20x2+600x+3500
=£®45£Ђx£≠40£©£®700£≠20x£©=-20x2+600x+3500
”…ћв“вњ…µ√£Ї![]()
љвµ√£Ї![]()
£®2£©![]() =-20x2+600x+3500=-20£®x£≠15£©2+8000£ђ∆д÷–-20£Љ0
=-20x2+600x+3500=-20£®x£≠15£©2+8000£ђ∆д÷–-20£Љ0
°аµ±x=15 ±£ђ![]() ”–„оіу÷µ£ђ„оіу÷µќ™8000
”–„оіу÷µ£ђ„оіу÷µќ™8000
ір£Їµ±√њЇ–’«Љџќ™15‘™ ±£ђ√њћмµƒѕъ џјы»у![]() „оіу£ђ„оіујы»у «8000‘™£Ѓ
„оіу£ђ„оіујы»у «8000‘™£Ѓ
£®3£©µ±![]() =6000 ±£ђ-20£®x£≠15£©2+8000=6000
=6000 ±£ђ-20£®x£≠15£©2+8000=6000
љвµ√£Їx1=5£ђx2=25
°я![]() =-20x2+600x+3500µƒњ™њЏѕтѕ¬
=-20x2+600x+3500µƒњ™њЏѕтѕ¬
°аµ±5°№x°№25 ±£ђP°Ё6000
ір£Їµ±5°№x°№25 ±£ђ≥ђ –ѕл“™√њћмїсµ√≤їµЌ”Џ6000‘™µƒјы»у£Ѓ


 њЏЋгћвњ®±±Њ©ЄЊ≈ЃґщЌѓ≥ц∞ж…зѕµЅ–ір∞Є
њЏЋгћвњ®±±Њ©ЄЊ≈ЃґщЌѓ≥ц∞ж…зѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њќ™ЅЋ”≠љ”ће”эјнїѓЉ” ‘£ђЊ≈£®2£©∞аЌђ—Іµљƒ≥ће”э”√∆Ј…ћµк≤…єЇ—µЅЈ”√«т£ђ“—÷™єЇ¬т3ЄцA∆Ј≈∆„г«тЇЌ2ЄцB∆Ј≈∆„г«т–иЄґ210‘™£їєЇ¬т2ЄцA∆Ј≈∆„г«тЇЌ1ЄцB∆Ј≈∆„г«т–иЄґЈ—130‘™£Ѓ£®”≈їЁіл ©ЉыЇ£±®£©

£®1£©«уA£ђBЅљ∆Ј≈∆„г«тµƒµ•ЉџЄчќ™ґа…ў‘™£ї
£®2£©ќ™ѕн №”≈їЁ£ђЌђ—І√«Њцґ®єЇ¬т“їіќ–‘єЇ¬т„г«т60Єц£ђ»ф“™«уA∆Ј≈∆„г«тµƒ эЅњ≤їµЌ”ЏB∆Ј≈∆„г«т эЅњµƒ3±ґ£ђ«лƒг…иЉ∆“ї÷÷ЄґЈ—„о…ўµƒЈљ∞Є£ђ≤ҐЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™≈„ќпѕяy£љ©Б![]() x2+bx+cЊ≠єэµгA£®4£ђ3£©£ђґ•µгќ™B£ђґ‘≥∆÷б «÷±ѕяx£љ2£Ѓ
x2+bx+cЊ≠єэµгA£®4£ђ3£©£ђґ•µгќ™B£ђґ‘≥∆÷б «÷±ѕяx£љ2£Ѓ
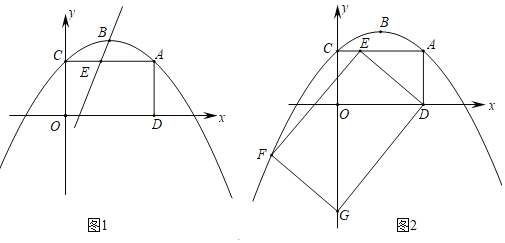
£®1£©«у≈„ќпѕяµƒЇѓ э±ніп љЇЌґ•µгBµƒ„ш±к£ї
£®2£©»зЌЉ1£ђ≈„ќпѕя”лy÷бљї”ЏµгC£ђЅђљ”AC£ђєэA„чAD°Ќx÷б”ЏµгD£ђE «ѕяґќAC…ѕµƒґѓµг£®µгE≤ї”лA£ђCЅљµг÷ЎЇѕ£©£ї
£®i£©»ф÷±ѕяBEљЂЋƒ±я–ќACODЈ÷≥…√жїэ±»ќ™1£Ї3µƒЅљ≤њЈ÷£ђ«уµгEµƒ„ш±к£ї
£®ii£©»зЌЉ2£ђЅђљ”DE£ђ„чЊЎ–ќDEFG£ђ‘ЏµгEµƒ‘Ћґѓєэ≥ћ÷–£ђ «Јсіж‘ЏµгG¬д‘Џy÷б…ѕµƒЌђ ±µгF«°Ї√¬д‘Џ≈„ќпѕя…ѕ£њ»фіж‘Џ£ђ«у≥ціЋ ±AEµƒ≥§£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
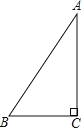
°Њћвƒњ°њ»зЌЉ£ђ“—÷™Rt°чABC÷–°ѕC=90°г£ђAB=10£ђAC=8£Ѓ
£®1£©„чABµƒіє÷±∆љЈ÷ѕяDE£ђљїAB”ЏµгD£ђљїAC”ЏµгE£Ѓ(“™«у≥яєж„чЌЉ£ђ≤ї–і„чЈ®£ђ±£Ѕф„чЌЉЇџЉ£)£ї
£®2£©«уAEµƒ≥§£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ’эЈљ–ќABCDµƒ±я≥§AB£љ8£ђEќ™∆љ√жƒЏ“їґѓµг£ђ«“AE£љ4£ђFќ™CD…ѕ“їµг£ђCF£љ2£ђЅђљ”EF£ђED£ђ‘т2EF+EDµƒ„о–°÷µќ™£®°°°°£©
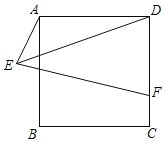
A.12![]() B.12
B.12![]() C.12D.10
C.12D.10
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
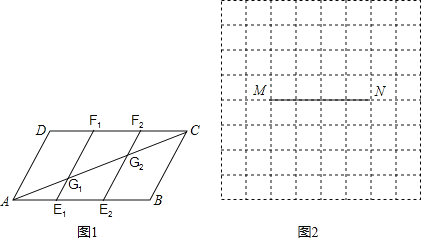
°Њћвƒњ°њ(1)»зЌЉ1£ђ‘Џ∆љ––Ћƒ±я–ќABCD÷–£ђµгE1£ђE2 «AB»эµ»Ј÷µг£ђµгF1£ђF2 «CD»эµ»Ј÷µг£ђE1F1£ђE2F2Ј÷±рљїAC”ЏµгG1£ђG2£ђ«у÷§£ЇAG1£љG1G2£љG2C£Ѓ
(2)»зЌЉ2£ђ”…64Єц±я≥§ќ™1µƒ–°’эЈљ–ќ„й≥…µƒ“їЄцЌшЄсЌЉ£ђѕяґќMNµƒЅљЄцґЋµг‘ЏЄсµг…ѕ£ђ«л”√“ї∞—ќёњћґ»µƒ≥я„”£ђї≠≥цѕяґќMN»эµ»Ј÷µгP£ђQ£Ѓ(±£Ѕф„чЌЉЇџЉ£)
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђRt°чACB÷–£ђ°ѕC=90°г£ђAC=6£ђBC=8£ђ∞лЊґќ™1µƒ°—O”лAC£ђBCѕа«–£ђµ±°—O—Ў±яCB∆љ“∆÷Ѕ”лABѕа«– ±£ђ‘т°—O∆љ“∆µƒЊајлќ™£®°°°°£©
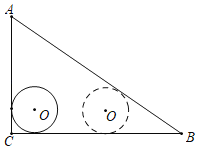
A.3B.4C.5D.6
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њќ™ќ»≤љЌ∆љш5GЌш¬зљ®…и£ђ…оїѓє≤љ®є≤ѕн£ђµ±Љ„ґ” ©є§20ћмЌк≥…5Gїщ’Њљ®…иє§≥ћµƒ![]() ±£ђ““ґ”Љ”»лЄ√є§≥ћ£ђљбєы±»Љ„ґ”µ•ґј ©є§ћб«∞25ћмЌк≥…ЅЋ £”аµƒє§≥ћ£Ѓ
±£ђ““ґ”Љ”»лЄ√є§≥ћ£ђљбєы±»Љ„ґ”µ•ґј ©є§ћб«∞25ћмЌк≥…ЅЋ £”аµƒє§≥ћ£Ѓ
(1)»ф““ґ”µ•ґј ©є§£ђ–и“™ґа…ўћм≤≈ƒ№Ќк≥…Є√ѕоє§≥ћ£њ
(2)»ф““ґ”≤ќ”лЄ√ѕоє§≥ћ ©є§µƒ ±Љд≤ї≥ђєэ12ћм£ђ‘тЉ„ґ”і”њ™ Љ ©є§µљЌк≥…Є√є§≥ћ÷Ѕ…ў–и“™ґа…ўћм£њ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ÷±ѕя![]() ”лЈі±»јэЇѓ э
”лЈі±»јэЇѓ э![]() µƒЌЉѕуљї”ЏA£®-1£ђ3£©£ђB£®3£ђ
µƒЌЉѕуљї”ЏA£®-1£ђ3£©£ђB£®3£ђ![]() £©Ѕљµг£ђєэµгA„чAC°Ќx÷б”ЏµгC£ђєэµгB„чBD°Ќx÷б”ЏµгD£Ѓ
£©Ѕљµг£ђєэµгA„чAC°Ќx÷б”ЏµгC£ђєэµгB„чBD°Ќx÷б”ЏµгD£Ѓ
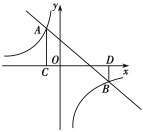
£®1£©«у“їіќЇѓ эЉ∞Јі±»јэЇѓ эµƒљвќц љ£ї
£®2£©»фµгP‘Џ÷±ѕя![]() …ѕ£ђ«“S°чACP£љ2S°чBDP£ђ«уµгPµƒ„ш±к£Ѓ
…ѕ£ђ«“S°чACP£љ2S°чBDP£ђ«уµгPµƒ„ш±к£Ѓ
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com