
【题目】如图,Rt△ACB中,∠C=90°,AC=6,BC=8,半径为1的⊙O与AC,BC相切,当⊙O沿边CB平移至与AB相切时,则⊙O平移的距离为( )
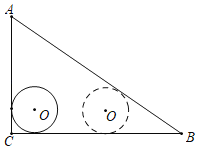
A.3B.4C.5D.6
【答案】B
【解析】
设⊙O与AC相切于D,与BC相切于H,平移后的⊙O′与AB相切于F,与BC相切于E,连接OH,O′D,则点O在O′D上,连接O′F,EO′并延长交AB于G,根据正方形和矩形的性质得到OD=OH=O′E=O′F=CD=CH=1,OO′=HE,根据相似三角形的判定和性质定理即可得到结论.
解:∵Rt△ACB中,∠C=90°,AC=6,BC=8,
∴AB=10,
设⊙O与AC相切于D,与BC相切于H,平移后的⊙O′与AB相切于F,与BC相切于E,
连接OH,O′D,则点O在O′D上,连接O′F,EO′并延长交AB于G,
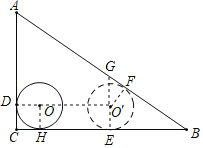
∴四边形CDOH是正方形,四边形OHEO′是矩形,
∴OD=OH=O′E=O′F=CD=CH=1,OO′=HE,
∴EG⊥BC,
∵∠C=90°,
∴EG∥AC,
∴∠FGE=∠A,
∵∠GFO′=∠C=90°,
∴∠O′FG∽∠BCA,
∴![]() ,
,
∴![]() ,
,
∴O′G=![]() ,
,
∴EG=![]() ,
,
∵GE∥AC,
∴△BGE∽△BAC,
∴![]() ,
,
∴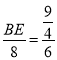 ,
,
∴BE=3,
∴OO′=HE=BC﹣CH﹣BE=8﹣1﹣3=4,
∴⊙O平移的距离为4,
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5G网络,是最新一代蜂窝移动通信技术,其数据传输速率远高于以前的蜂窝网络,最高可达10Gbit/s,比4G快100倍.5G手机也成为生活、工作不可缺少的移动设备,某电商公司销售两种5G手机,已知售出5部A型手机,3部B型手机的销售额为51000元;售出3部A型手机,2部B型手机的销售额为31500元.
(1)求A型手机和B型手机的售价分别是多少元;
(2)该电商公司在3月实行“满减促销”活动,活动方案为:单部手机满3000元减500元,满5000元减1500元(每部手机只能参加最高满减活动),结果3月A型手机的销量是B型手机的![]() ,4月该电商公司加大促销活动力度,每部A型手机按照3月满减后的售价再降
,4月该电商公司加大促销活动力度,每部A型手机按照3月满减后的售价再降![]() a%,销量比3月增加2a%;每部B型手机按照满减后的售价再降a%,销量比3月销量增加
a%,销量比3月增加2a%;每部B型手机按照满减后的售价再降a%,销量比3月销量增加![]() a%,结果4月的销售总额比3月的销售总额多
a%,结果4月的销售总额比3月的销售总额多![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在中秋节来临前夕,购进一种品牌月饼,每盒进价是40元,超市规定每盒售价不得少于45元,根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)请写出每天的销售利润![]() (元)与每盒涨价
(元)与每盒涨价![]() (元)之间的函数关系式及自变量
(元)之间的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)当每盒涨价为多少元时,每天的销售利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
(3)如果超市想要每天获得不低于6000元的利润,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
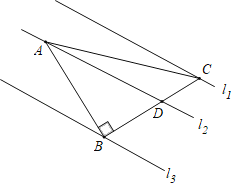
【题目】如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,BC交l2于D点.
(1)求AB的长.
(2)求sin∠BAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
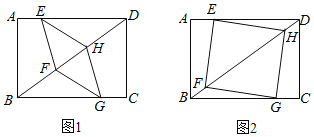
【题目】矩形ABCD,AB=6,BC=8,四边形EFGH的顶点E、G在矩形的边AD、BC上;顶点F、H在矩形的对角线BD上.
(1)如图1,当四边形EFGH是平行四边形时,求证:△DEH≌△BGF.
(2)如图2,当四边形EFGH是正方形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
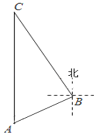
【题目】我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在 A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( ).(参考数据sin53°≈0.80,cos53°≈0.60)
A.12千米B.(3+4![]() )千米C.(3+5
)千米C.(3+5![]() )千米D.(12﹣4
)千米D.(12﹣4![]() )千米
)千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=3.点E在线段BA上从B点以每秒1个单位的速度出发向A点运动,F是射线CD上一动点,在点E、F运动的过程中始终保持EF=5,且CF>BE,点P是EF的中点,连接AP.设点E运动时间为ts.



(1)在点E、F运动的过程中,AP的长度存在一个最小值,当AP的长度取得最小值时,点P的位置应该在 .
(2)当AP⊥EF时,求出此时t的值
(3)以P为圆心作⊙P,当⊙P与矩形ABCD三边所在直线都相切时,求出此时t的值,并指出此时⊙P的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
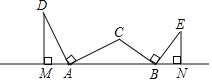
【题目】如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com