
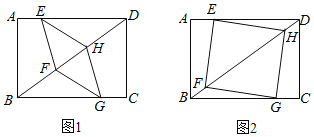
【题目】矩形ABCD,AB=6,BC=8,四边形EFGH的顶点E、G在矩形的边AD、BC上;顶点F、H在矩形的对角线BD上.
(1)如图1,当四边形EFGH是平行四边形时,求证:△DEH≌△BGF.
(2)如图2,当四边形EFGH是正方形时,求BF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由EH=FG,∠BFG=∠EHD,∠EDH=∠GBF,即可证明;
(2)证明△HKG≌△GMF(AAS),利用BC=BM+MG+GK+KC=8,即可求解.
解:在Rt△BCD中,tan∠DBC=![]()
![]()
=tanα,则sin![]() ,cosα=
,cosα=![]() ,
,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDH=∠GBF,
(1)∵四边形EFGH是平行四边形,
∴EH=FG,∠EHF=∠GFH,
∴∠BFG=180°﹣∠GFH,∠EHD=180°﹣∠EHF=∠BFG,
又∵∠EDH=∠GBF,
∴△DEH≌△BGF(AAS);
(2)∵四边形EFGH是正方形也为平行四边形,
故由(1)得:△DEH≌△BGF(AAS),
∴BF=DH,
设BF=x=DH,
如下图,过点H作HK⊥BC于点K,作HN⊥CD于点N,作FM⊥BC于点M,
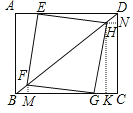
在Rt△BFM中,FM=BFsin∠FBM=xsinα=![]() =DN,
=DN,
同理BM=![]() =HN=CK,
=HN=CK,
∵∠FGM+∠HGK=90°,∠HGK+∠GHK=90°,
∴∠GHK=∠FGM,
又∵∠HKG=∠GMF=90°,FG=GH,
∴△HKG≌△GMF(AAS),
∴GM=HK=CN=CD﹣DN=6﹣![]() ,GK=FM=
,GK=FM=![]() ,
,
∴BC=BM+MG+GK+KC=![]() +(6﹣
+(6﹣![]() )+
)+![]() =8,
=8,
解得:x=![]() ,
,
即BF的长为![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
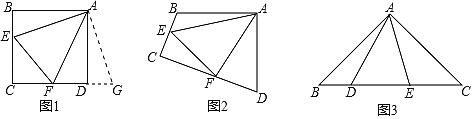
【题目】探究:如图1和图2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
(1)①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系 ;
②如图2,若∠B、∠D都不是直角,但满足∠B+∠D=180°,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2![]() .点D、E均在边BC边上,且∠DAE=45°,若BD=1,求DE的长.
.点D、E均在边BC边上,且∠DAE=45°,若BD=1,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
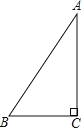
【题目】如图,已知Rt△ABC中∠C=90°,AB=10,AC=8.
(1)作AB的垂直平分线DE,交AB于点D,交AC于点E.(要求尺规作图,不写作法,保留作图痕迹);
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
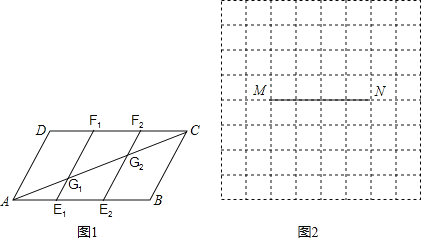
【题目】(1)如图1,在平行四边形ABCD中,点E1,E2是AB三等分点,点F1,F2是CD三等分点,E1F1,E2F2分别交AC于点G1,G2,求证:AG1=G1G2=G2C.
(2)如图2,由64个边长为1的小正方形组成的一个网格图,线段MN的两个端点在格点上,请用一把无刻度的尺子,画出线段MN三等分点P,Q.(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
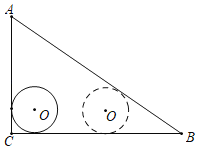
【题目】如图,Rt△ACB中,∠C=90°,AC=6,BC=8,半径为1的⊙O与AC,BC相切,当⊙O沿边CB平移至与AB相切时,则⊙O平移的距离为( )
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题错误的是( ).
A.弦的垂直平分线必平分弦所对的两条弧.
B.掷一枚均匀的骰子,骰子停止转动后,2点朝上是随机事件.
C.若Rt△ABC的两边长恰为方程x2-7x+12=0的两个实数根,则其斜边长为5.
D.若直线y=ax-b与直线y=mx+n交于点(2,-1),则方程![]() 的解为
的解为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为稳步推进5G网络建设,深化共建共享,当甲队施工20天完成5G基站建设工程的![]() 时,乙队加入该工程,结果比甲队单独施工提前25天完成了剩余的工程.
时,乙队加入该工程,结果比甲队单独施工提前25天完成了剩余的工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若乙队参与该项工程施工的时间不超过12天,则甲队从开始施工到完成该工程至少需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
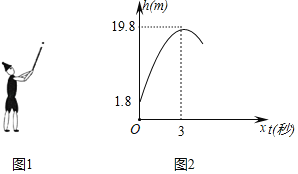
【题目】如图1,皮皮小朋友燃放一种手持烟花,这种烟花每隔2秒发射一发花弹,每一发花弹的飞行路径,爆炸时的高度均相同,皮皮小朋友发射出的第一发花弹的飞行高度![]() (米)与飞行时间
(米)与飞行时间![]() (秒)之间的函数图像如图2所示.
(秒)之间的函数图像如图2所示.
(1)求皮皮发射出的第一发花弹的飞行高度![]() (米)与飞行时间
(米)与飞行时间![]() (秒)之间的函数关系式;
(秒)之间的函数关系式;
(2)第一发花弹发射3秒后,第二发花弹达到的高度为多少米?
(3)为了安全,要求花弹爆炸时的高度不低于16米,皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
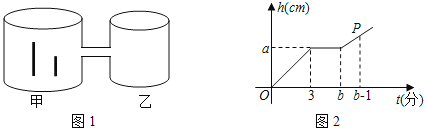
【题目】如图1是两圆柱形连通容器,两根铁棒直立于甲容器底部(连通处及铁棒体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)与时间t(分)的函数关系如图2所示.已知两根铁棒的长度之和为34cm,当水面达到连通处时,一根露出水面的长度是它的![]() ,另一根露出水面的长度是它的
,另一根露出水面的长度是它的![]() .
.
(1)①图2中(3,a)表示的实际意义是 ;
②请求出a的值;
(2)若甲、乙两容器的底面积之比为S甲,S乙=3:2.
①直接写出b的值为 ;
②求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com