
【题目】如图1是两圆柱形连通容器,两根铁棒直立于甲容器底部(连通处及铁棒体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)与时间t(分)的函数关系如图2所示.已知两根铁棒的长度之和为34cm,当水面达到连通处时,一根露出水面的长度是它的![]() ,另一根露出水面的长度是它的
,另一根露出水面的长度是它的![]() .
.
(1)①图2中(3,a)表示的实际意义是 ;
②请求出a的值;
(2)若甲、乙两容器的底面积之比为S甲,S乙=3:2.
①直接写出b的值为 ;
②求点P的坐标.
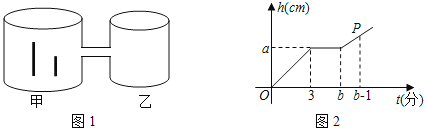
【答案】(1)①注水3分钟后甲容器的水面高度达到联通处;②a=12;(2)①5;②(6,![]() ).
).
【解析】
(1)①根据图示表示的意义解答即可;②根据题意列出方程解答即可;
(2)①根据图示得出B的值即可;②根据题意得出比例关系解答即可.
解:(1)①(3,a)表示的实际意义是注水3分钟后甲容器的水面高度达到联通处;
②由题意,两根铁棒长度分别为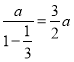 ,
,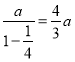 ,
,
可得:![]() ,
,
解得:a=12,
(2)①b=5;
②由题意b+1=6,5分钟时甲乙容器的水面高度都达到联通处,此时水面高为12,
设S甲=3k,S乙=2k,则每分钟注水体积![]() ,
,
∴6分钟时水面高为![]() ,
,
∴即点P的坐标为(6,![]() ).
).
故答案为:注水3分钟后甲容器的水面高度达到联通处;5.


科目:初中数学 来源: 题型:
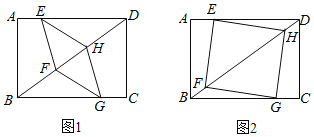
【题目】矩形ABCD,AB=6,BC=8,四边形EFGH的顶点E、G在矩形的边AD、BC上;顶点F、H在矩形的对角线BD上.
(1)如图1,当四边形EFGH是平行四边形时,求证:△DEH≌△BGF.
(2)如图2,当四边形EFGH是正方形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是![]() ;③△ADF与△EBF的面积比为3:2,④△ABF的面积为
;③△ADF与△EBF的面积比为3:2,④△ABF的面积为![]() ,其中一定成立的有( )个.
,其中一定成立的有( )个.
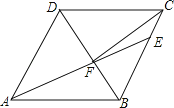
A.2B.3C.1D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=12cm,BC=16cm,AB=20cm,∠CAB的角平分线AD交BC于点D.
(1)根据题意将图形补画完整(要求:尺规作图保留作图痕迹,不写作法);
(2)求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM=_____.
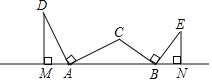
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1(2,1)在直线y=kx上,过点A1作A1B1∥y轴交x轴于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=kx和x轴于A2,B2两点,以点A2为直角顶点,,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则带点Cn的坐标为_________________.(结果用含正整数n的代数式表示)
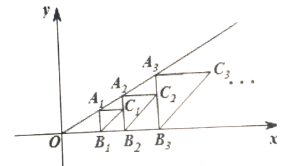
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴交于点A,与y轴交于点B,抛物线y=﹣
x+4与x轴交于点A,与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A,B两点,与x轴正半轴交于点C,连接BC,P为线段AC上的动点,P与A,C不重合,作PQ∥BC交AB于点Q,A关于PQ的对称点为D,连接PD,QD,BD.
x2+bx+c经过A,B两点,与x轴正半轴交于点C,连接BC,P为线段AC上的动点,P与A,C不重合,作PQ∥BC交AB于点Q,A关于PQ的对称点为D,连接PD,QD,BD.
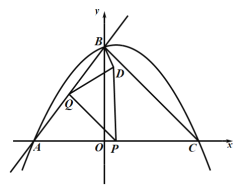
(1)求抛物线的解析式;
(2)当点D在抛物线上时,求点P的坐标.
(3)设点P的横坐标为x,△PDQ与△ABC的重叠部分的面积为S
①直接写出S与x的函数关系式;
②当△BDQ为直角三角形时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去超市采购防疫物品,超市提供下表所示![]() 、
、![]() 两种套餐,小明决定购买50份
两种套餐,小明决定购买50份![]() 套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐类别 | 一次性防护口罩 | 免洗洗手液 | 套餐价格 |
| 2包 | 1瓶 | 71元 |
| 1包 | 2瓶 | 67元 |
(1)求一次性防护口罩和免洗洗手液各自的单价;
(2)小明觉得优惠方式二比方式一的优惠力度更大,他计划分两次购买,第一次付现金购买一部分![]() 套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市快递员的收入情况,现随机抽取了甲、乙两家快递公司50天的送货单,对两个公司的快递员人均每天的送货单数进行统计,数据如下:
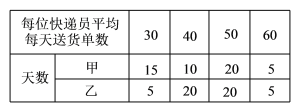
已知这两家快递公司的快递员的日工资方案 为:甲公司规定底薪70元,每单抽成1 元;乙公司规定底薪90元,每日前40单无抽成,超过40单的部分每单抽成3元.
(1)现从这50天中随机抽取1天,求这一天乙公司快递员人均送货单数超过40(不含40)单的概率;
(2)根据以上统计数据,若将各公司快递员的人均送货单数视为该公司各快递员的送货单数,
①估计甲快递公可各快递员的日均送货单数:
②小明拟到甲、乙两家快递公司中的一家应聘快递员的工作.如果仅从工资收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com