
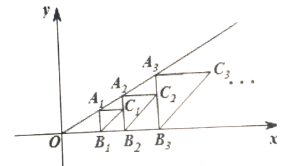
����Ŀ����ͼ����A1��2��1����ֱ��y=kx�ϣ�����A1��A1B1��y�ύx���ڵ�B1���Ե�A1Ϊֱ�Ƕ��㣬A1B1Ϊֱ�DZ���A1B1���Ҳ�������ֱ�ǡ�A1B1C1���ٹ���C1��A2B2��y�ᣬ�ֱ�ֱ��y=kx��x����A2��B2���㣬�Ե�A2Ϊֱ�Ƕ��㣬��A2B2Ϊֱ�DZ���A2B2���Ҳ�������ֱ�ǡ�A2B2C2�������˹��ɽ�����ȥ�������Cn������Ϊ_________________��������ú�������n�Ĵ���ʽ��ʾ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������(����)��
A.�ҵĴ�ֱƽ���߱�ƽ�������Ե���������
B.��һö���ȵ����ӣ�����ֹͣת����2�㳯��������¼���
C.��Rt��ABC�����߳�ǡΪ����x2-7x+12=0������ʵ����������б�߳�Ϊ5��
D.��ֱ��y=ax-b��ֱ��y=mx+n���ڵ�(2��-1)����![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ
Ϊ![]() ��һ�㣬������
��һ�㣬������![]() ��
��![]() ��
��![]() �ֱ�
�ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ������
������![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
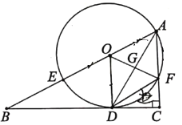
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() �����ú�
�����ú�![]() ��
��![]() �Ĵ���ʽ��ʾ�߶�
�Ĵ���ʽ��ʾ�߶�![]() �ij���
�ij���
��3����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
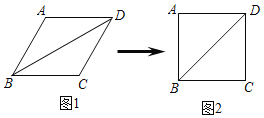
����Ŀ��С�����ĸ�������ͬ��ľ����β����������ܹ����ѧ�ߣ����Ȼѧ�߳�Ϊͼ1��ʾ������á�B��60�㣬���Żѧ�߳�Ϊͼ2��ʾ������á�ABC��90�㣬��ͼ2�Խ���BD��40cm����ͼ1�жԽ���BD�ij�Ϊ��������
A.20cmB.20![]() cmC.20
cmC.20![]() cmD.20
cmD.20![]() cm
cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
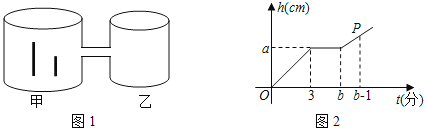
����Ŀ����ͼ1����Բ������ͨ��������������ֱ���ڼ������ײ�����ͨ��������������Բ��ƣ��������������עˮ����������ˮ��߶�h��cm����ʱ��t���֣��ĺ�����ϵ��ͼ2��ʾ����֪���������ij���֮��Ϊ34cm����ˮ��ﵽ��ͨ��ʱ��һ��¶��ˮ��ij���������![]() ����һ��¶��ˮ��ij���������
����һ��¶��ˮ��ij���������![]() ��
��
��1����ͼ2�У�3��a����ʾ��ʵ���������� ����
�������a��ֵ��
��2�����ס����������ĵ����֮��ΪS����S����3��2��
��ֱ��д��b��ֵΪ�� ����
�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij����ʵʩ��ҵ����ƶ������ƶ�����а�������Ķ������ֲ��Ʒ��ݮ����֪�ò�ݮ�ijɱ�Ϊÿǧ��10Ԫ����ݮ�����Ͷ���г����ۣ����г����鷢�֣���ݮ���۲����������ÿ���������y��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�֮�亯����ϵ��ͼ��ʾ��

��1����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2������Ʒ�ֲ�ݮ�Ķ���Ϊ����ʱ��ÿ�����ۻ�����������������Ƕ��٣�
��3��ij������ݮ��ժ����30�죬Ԥ�Ʋ���6000ǧ�ˣ����գ�2���еķ�ʽ�������ۣ��ܷ�������������ݮ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���мס������ֿͳ���2�����ֿͳ���3�����ֿͳ������ؿ���Ϊ180�ˣ�1�����ֿͳ���2�����ֿͳ������ؿ���Ϊ105�ˣ�
��1������1�����ֿͳ���1�����ֿͳ����ؿ����ֱ�Ϊ�����ˣ�
��2��ijѧУ��֯240��ʦ�����������������üס������ֿͳ���6����һ�ν�ȫ��ʦ���͵�ָ���ص㣮��ÿ�����ֿͳ������Ϊ400Ԫ��ÿ�����ֿͳ������Ϊ280Ԫ����������ʡ���õ���������������ͷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
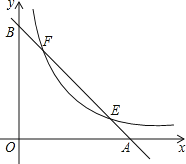
����Ŀ����ͼ����ֱ֪��y����x+2�ֱ���x�ᣬy�ύ��A��B���㣬��˫����y��![]() ����E��F���㣬��AB��2EF����k��ֵ��_____��
����E��F���㣬��AB��2EF����k��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
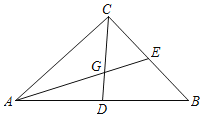
����Ŀ����֪����ͼ����Rt��ABC�У���ACB��90����BC��12��cosB��![]() ��D��E�ֱ���AB��BC���ϵ��е㣬AE��CD�ཻ�ڵ�G��
��D��E�ֱ���AB��BC���ϵ��е㣬AE��CD�ཻ�ڵ�G��
��1����CG�ij���
��2����tan��BAE��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com