
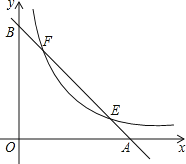
【题目】如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y=![]() 交于E,F两点,若AB=2EF,则k的值是_____.
交于E,F两点,若AB=2EF,则k的值是_____.
【答案】![]() .
.
【解析】
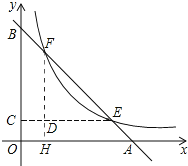
作FH⊥x轴,EC⊥y轴,FH与EC交于D,先利用一次函数图像上的点的坐标特征得到A点(2,0),B点(0,2),易得△AOB为等腰直角三角形,则AB=2![]() ,所以,EF=
,所以,EF=![]() AB=
AB=![]() ,且△DEF为等腰直角三角形,则FD=DE=
,且△DEF为等腰直角三角形,则FD=DE=![]() EF=1,设F点坐标是:(t,﹣t+2),E点坐标为(t+1,﹣t+1),根据反比例函数图象上的点的坐标特征得到t(﹣t+2)=(t+1)(﹣t+1),解得t=
EF=1,设F点坐标是:(t,﹣t+2),E点坐标为(t+1,﹣t+1),根据反比例函数图象上的点的坐标特征得到t(﹣t+2)=(t+1)(﹣t+1),解得t=![]() ,则E点坐标为(
,则E点坐标为(![]() ,
,![]() ),继而可求得k的值.
),继而可求得k的值.
如图,作FH⊥x轴,EC⊥y轴,FH与EC交于D,
由直线y=﹣x+2可知A点坐标为(2,0),B点坐标为(0,2),OA=OB=2,
∴△AOB为等腰直角三角形,
∴AB=2![]() ,
,
∴EF=![]() AB=
AB=![]() ,
,
∴△DEF为等腰直角三角形,
∴FD=DE=![]() EF=1,
EF=1,
设F点横坐标为t,代入y=﹣x+2,则纵坐标是﹣t+2,则F的坐标是:(t,﹣t+2),E点坐标为(t+1,﹣t+1),
∴t(﹣t+2)=(t+1)(﹣t+1),解得t=![]() ,
,
∴E点坐标为(![]() ,
,![]() ),
),
∴k=![]() ×
×![]() =
=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
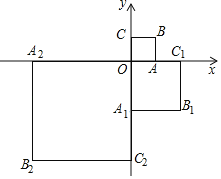
【题目】如图,在平面直角坐标系xOy中,正方形OABC的顶点A、C分别在x,y轴上,且AO=1.将正方形OABC绕原点O顺时针旋转90°,且A1O=2AO,得到正方形OA1B1C1,再将正方OA1B1C1绕原点O顺时针旋转90°,且A2O=2A1O,得到正方形OA2B2C2…以此规律,得到正方形OA2019B2019C2019,则点B2019的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
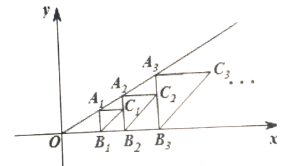
【题目】如图,点A1(2,1)在直线y=kx上,过点A1作A1B1∥y轴交x轴于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=kx和x轴于A2,B2两点,以点A2为直角顶点,,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则带点Cn的坐标为_________________.(结果用含正整数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
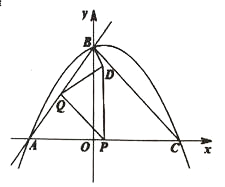
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,连接
,连接![]() ,
,![]() 为线段
为线段![]() 上的动点,
上的动点,![]() 与
与![]() ,
,![]() 不重合,作
不重合,作![]() 交
交![]() 于
于![]() ,
,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在抛物线上时,求点
在抛物线上时,求点![]() 的坐标;
的坐标;
(3)设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
①直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
②当![]() 为直角三角形时,直接写出
为直角三角形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去超市采购防疫物品,超市提供下表所示![]() 、
、![]() 两种套餐,小明决定购买50份
两种套餐,小明决定购买50份![]() 套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐类别 | 一次性防护口罩 | 免洗洗手液 | 套餐价格 |
| 2包 | 1瓶 | 71元 |
| 1包 | 2瓶 | 67元 |
(1)求一次性防护口罩和免洗洗手液各自的单价;
(2)小明觉得优惠方式二比方式一的优惠力度更大,他计划分两次购买,第一次付现金购买一部分![]() 套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受非洲猪瘟疫情感染受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
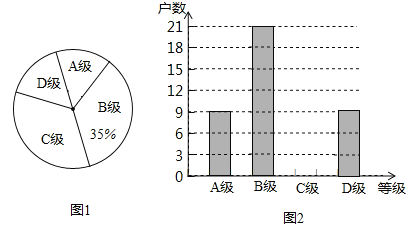
(1)本次抽样调查的养殖户的总户数是 ;把图2条形统计图补充完整.
(2)若该地区建档的养殖户有1500户,求非常严重与严重的养殖户一共有多少户?
(3)某调研单位想从5户建档养殖户(分别记为a,b,c,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
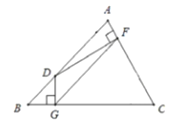
【题目】已知:△ABC中,∠B=45°,∠C=60°,BC=4,D、F分别为AB、AC边上的一个动点,过D分别作DF⊥AC于F,DG⊥BC于G,那么FG的最小值为()
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com