
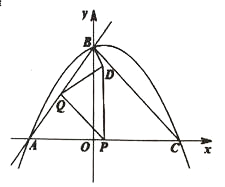
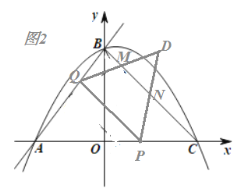
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,连接
,连接![]() ,
,![]() 为线段
为线段![]() 上的动点,
上的动点,![]() 与
与![]() ,
,![]() 不重合,作
不重合,作![]() 交
交![]() 于
于![]() ,
,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在抛物线上时,求点
在抛物线上时,求点![]() 的坐标;
的坐标;
(3)设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
①直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
②当![]() 为直角三角形时,直接写出
为直角三角形时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)P(1,0);(3)①当-3<x≤
;(2)P(1,0);(3)①当-3<x≤![]() 时,S=
时,S=![]() ;当
;当![]() <x<4时,S=
<x<4时,S=![]() ;②
;②![]() 的值是
的值是![]() 或
或![]() .
.
【解析】
(1)求出点A,B坐标,代入抛物线![]() 解析式,解关于b,c的方程组即可;
解析式,解关于b,c的方程组即可;
(2)设点P(x,0),易得OB=OC,得到∠BCP=45°,由![]() ,得∠QPA=∠BCO=45°,从而有∠APD=90°,故D(x,x+3),代入解析式
,得∠QPA=∠BCO=45°,从而有∠APD=90°,故D(x,x+3),代入解析式![]() 即可得解.
即可得解.
(3)①分两种情况i)当点P在线段AC的中点左侧时,![]() 始终在
始终在![]() 内部,ii)当点p在线段AC的中点右侧时,
内部,ii)当点p在线段AC的中点右侧时,![]() 有部分在
有部分在![]() 外部,然后分别计算重叠部分的面积求解即可.②分∠QDB=90°与∠QBD=90°,由PQ∥BC,得到
外部,然后分别计算重叠部分的面积求解即可.②分∠QDB=90°与∠QBD=90°,由PQ∥BC,得到![]() ,得到
,得到![]() QB=
QB=![]() ,又BD=
,又BD=![]() ,利用勾股定理建立方程求解即可.
,利用勾股定理建立方程求解即可.
(1)令x=0,则y=4,令y=0,则x=-3
∴A(-3,0)B(0,4)∵抛物线![]() 经过A,B两点,
经过A,B两点,
∴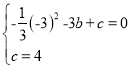
解得![]() ,c=4
,c=4
∴![]()
(2)设P点坐标为(x,0)
令![]() =0
=0
解得![]()
∴OB=OC=4
∴∠BCO=45°
又PQ∥BC
∴∠QPA=∠BCO=45°
∴∠APD=90°
∴D(x,x+3)
∴![]() ,解得
,解得![]()
∵P与A,C不重合
∴P(1,0)
(3)为便与计算,先设点P的坐标为(m,0),又PQ∥BC,则直线PQ的解析式为y=-x-m,
由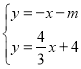 解得:
解得:![]() ,即
,即![]() ,
,
则![]()
![]() =
=![]()
i)当点P在线段AC的中点的左侧时,即-3<m≤![]() ,
,![]() 始终在
始终在![]() 内部,
内部,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() =
=![]() =
=![]() =
=![]() ,
,
ii)当点P在线段AC的中点的右侧时,即![]() <m<4,
<m<4,![]() 有部分在
有部分在![]() 外部,如图2所示,∵PQ∥BC,易知
外部,如图2所示,∵PQ∥BC,易知![]() ∽
∽![]() ,∴
,∴![]() (
(![]() ,
,![]() 分别为PQ,BC上的高,)∴易得
分别为PQ,BC上的高,)∴易得![]() 的边MN上的高与
的边MN上的高与![]() 边PQ上的高之比为
边PQ上的高之比为![]() ,又∵
,又∵![]() ∽
∽![]() ,∴
,∴![]() ,
,![]() =
=![]()
![]() ,
,
∴![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() =
=![]() -
-![]() =
=![]() -
-![]()
![]() =
=
![]() ,
,
∵点P(x,0),将上面式子中的m换为x即可.
②∵∠AQP=∠PQD=∠ABC=45°,
∴∠AQD>90°,
∴∠BQD≠90°,
i)当∠QDB=90°时,
设P(x,0),则D(x,x+3),AP=x+3,且易知AB=5,AC=7
又PQ∥BC
∴![]() ,
,
∴AQ=![]()
∴QB=![]() ,
,
又∵B(0,4),D(x,x+3),
∴BD=![]() ,
,
∵∠QDB=90°,
∴![]()
∴![]()
整理得:![]()
解之得:![]() (与点A重合,舍),
(与点A重合,舍),
∴P(![]() ,0)
,0)
ii)若∠QBD=90°,
同理:![]()
∴![]()
整理得:![]()
解之得:![]() (与点C重合,舍)
(与点C重合,舍)
∴P(![]() ,0)
,0)
∴当△BDQ为直角三角形时,![]() 的值是
的值是![]() 或
或![]() .
.
∴ 综上① i)当-3<x≤![]() 时,S=
时,S=![]() , ii)当
, ii)当![]() <x<4时,S=
<x<4时,S=![]()
②当△BDQ为直角三角形时,![]() 的值是
的值是![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
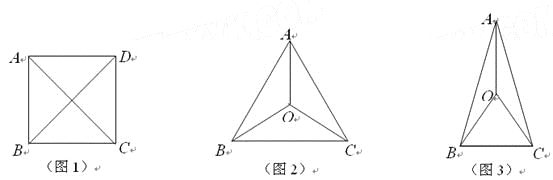
【题目】在平面上有且只有4个点,这4个点中有一个独特的性质:连结每两点可得到6条线段,这6条线段有且只有两种长度.我们把这四个点称作准等距点.例如正方形ABCD的四个顶点(如图1),有AB=BC=CD=DA,AC=BD.其实满足这样性质的图形有很多,如图2中A、B、C、O四个点,满足AB=BC=CA,OA=OB=OC;如图3中A、B、C、O四个点,满足OA=OB=OC=BC,AB=AC.
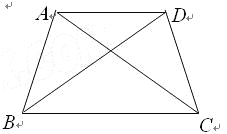
(1)如图,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.
①写出相等的线段(不再添加字母);
②求∠BCD的度数.
(2)请再画出一个四边形,使它的四个顶点为准等距点,并写出相等的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
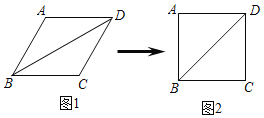
【题目】小明用四根长度相同的木条首尾相接制作了能够活动的学具,他先活动学具成为图1所示,并测得∠B=60°,接着活动学具成为图2所示,并测得∠ABC=90°,若图2对角线BD=40cm,则图1中对角线BD的长为( )
A.20cmB.20![]() cmC.20
cmC.20![]() cmD.20
cmD.20![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某乡镇实施产业精准扶贫,帮助贫困户承包了若干亩土地种植新品草莓,已知该草莓的成本为每千克10元,草莓成熟后投入市场销售,经市场调查发现,草莓销售不会亏本,且每天的销售量y(千克)与销售单价x(元/千克)之间函数关系如图所示.

(1)求y与x的函数关系式,并写出x的取值范围.
(2)当该品种草莓的定价为多少时,每天销售获得利润最大?最大利润是多少?
(3)某村今年草莓采摘期限30天,预计产量6000千克,则按照(2)中的方式进行销售,能否销售完这批草莓?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中为了了解学生的视力情况,从三个年级随机抽取了部分学生进行调查,并制作了下面的统计表和统计图.
各年级抽查学生视力各等第人数分布统计表
优秀 | 良好 | 合格 | 不合格 | |
七年级 |
| 20 | 22 | 23 |
八年级 | 11 | 17 | 13 | 19 |
九年级 | 8 |
| 11 | 25 |
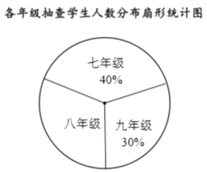
(1)在统计表中,![]() ________,
________,![]() ________;
________;
(2)在扇形统计图中,八年级所对应的扇形圆心角为________°;
(3)若该校三个年级共有1800名学生,试估计该校学生视力等第不合格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
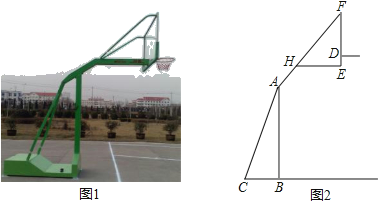
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为和点A'.
(1)以点A'为顶点求作△A'B'C',使△A'B'C'∽△ABC,S△A'B'C'=4S△ABC;
(尺规作图,保留作图痕迹,不写作法)
(2)设D、E、F分别是△ABC三边AB、BC、AC的中点,D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、A'C'的中点,求证:△DEF∽△D'E'F'.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com