
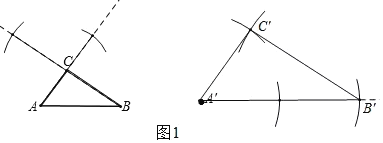
【题目】如图,已知△ABC为和点A'.
(1)以点A'为顶点求作△A'B'C',使△A'B'C'∽△ABC,S△A'B'C'=4S△ABC;
(尺规作图,保留作图痕迹,不写作法)
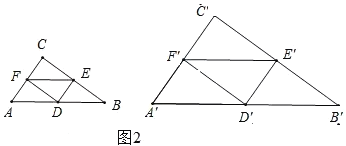
(2)设D、E、F分别是△ABC三边AB、BC、AC的中点,D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、A'C'的中点,求证:△DEF∽△D'E'F'.

【答案】(1)作图见解析;(2)证明见解析.
【解析】
(1)分别作A'C'=2AC、A'B'=2AB、B'C'=2BC得△A'B'C'即可.
(2)根据中位线定理易得△DEF∽△CAB,△D'E'F'∽△C'A'B',故可得△DEF∽△D'E'F'.
解:(1)作线段A'C'=2AC、A'B'=2AB、B'C'=2BC,得△A'B'C'即为所求.
证明:∵A'C'=2AC、A'B'=2AB、B'C'=2BC,
∴△ABC∽△A′B′C′,
∴![]() ;
;
(2)证明:∵D、E、F分别是△ABC三边AB、BC、AC的中点,
∴DE=![]() AC,DF=
AC,DF=![]() BC,EF=
BC,EF=![]() AB,
AB,
∴△DEF∽△CAB,
同理:△D'E'F'∽△C'A' B',
由(1)可知:△ABC∽△A′B′C′,
∴△DEF∽△D'E'F'.


科目:初中数学 来源: 题型:
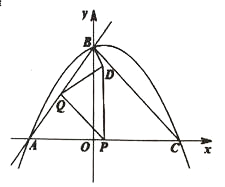
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,连接
,连接![]() ,
,![]() 为线段
为线段![]() 上的动点,
上的动点,![]() 与
与![]() ,
,![]() 不重合,作
不重合,作![]() 交
交![]() 于
于![]() ,
,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在抛物线上时,求点
在抛物线上时,求点![]() 的坐标;
的坐标;
(3)设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
①直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
②当![]() 为直角三角形时,直接写出
为直角三角形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解全国中学生视力的情况,应采用普查的方式
B.某种彩票中奖的概率是![]() ,买1000张这种彩票一定会中奖
,买1000张这种彩票一定会中奖
C.从2000名学生中随机抽取200名学生进行调查,样本容量为200名学生
D.从只装有白球和绿球的袋中任意摸出一个球,摸出黑球是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
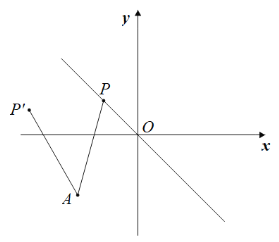
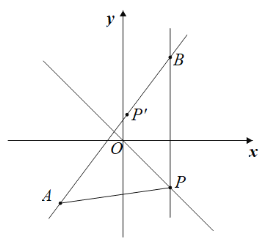
【题目】如图1,点P(m,n)在一次函数![]() 的图像上,将点P绕点A(
的图像上,将点P绕点A(![]()
![]() ,
,![]() )逆时针旋转45°,旋转后的对应点为P.
)逆时针旋转45°,旋转后的对应点为P.
(1)当![]() 时,求点P的坐标;
时,求点P的坐标;
(2)试说明:不论m为何值,点P的纵坐标始终不变;
(3)如图2,过点P作x轴的垂线交直线AP于点B,若直线PB与二次函数![]() 的图像交于点Q,当m>0时,试判断点B是否一定在点Q的上方,请说明理由.
的图像交于点Q,当m>0时,试判断点B是否一定在点Q的上方,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2![]() EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )

A. 14SB. 13SC. 12SD. 11S
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
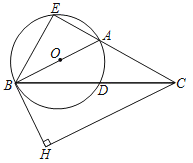
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D.延长CA交⊙O于点E,BH是⊙O的切线,作CH⊥BH.垂足为H.
(1)求证:BE=BH;
(2)若AB=5,tan∠CBE=2,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com